
【题目】如图,![]() 为
为![]() 的内接三角形,
的内接三角形,![]() 为
为![]() 的直径,过点
的直径,过点![]() 作
作![]() 的切线交
的切线交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() ,求证:
,求证:![]() ;
;
(3)若点![]() 为直径
为直径![]() 下方半圆的中点,连接
下方半圆的中点,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,
,![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
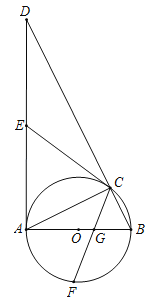
(1)利用AB是圆O的直径和AD是圆O的切线判断出∠ACD=∠DAB=90°,即可得出结论;
(2)利用切线长定理判断出AE=CE,从而得到∠DAC=∠EAC,再用等角的余角相等判断出∠D=∠DCE,得出DE=CE,即可得到结论;
(3)先求出tan∠ABD的值,进而得出GH=2CH,进而得到BC=3BH,再求出BC建立方程求BH,从而求出GH.
(1)∵AB是⊙O直径,∴∠ACD=∠ACB=90°.
∵AD是⊙O的切线,∴∠BAD=90°,∴∠ACD=∠DAB=90°.
∵∠D=∠D,∴△DAC∽△DBA;
(2)∵EA,EC是⊙O的切线,∴AE=CE(切线长定理),∴∠DAC=∠ECA.
∵∠ACD=90°,∴∠ACE+∠DCE=90°,∠DAC+∠D=90°,∴∠D=∠DCE,∴DE=CE,∴AD=AE+DE=CE+CE=2CE,∴CE![]() AD;
AD;
(3)如图,在Rt△ABD中,AD=6,AB=3,∴tan∠ABD![]() 2,过点G作GH⊥BD于H,∴tan∠ABD
2,过点G作GH⊥BD于H,∴tan∠ABD![]() 2,∴GH=2BH.
2,∴GH=2BH.
∵点F是直径AB下方半圆的中点,∴∠BCF=45°,∴∠CGH=∠CHG﹣∠BCF=45°,∴CH=GH=2BH,∴BC=BH+CH=3BH.在Rt△ABC中,tan∠ABC![]() 2,∴AC=2BC,根据勾股定理得:AC2+BC2=AB2,∴4BC2+BC2=9,∴BC
2,∴AC=2BC,根据勾股定理得:AC2+BC2=AB2,∴4BC2+BC2=9,∴BC![]() ,∴3BH
,∴3BH![]() ,∴BH
,∴BH![]() ,∴GH=2BH
,∴GH=2BH![]() .在Rt△CHG中,∠BCF=45°,∴CG
.在Rt△CHG中,∠BCF=45°,∴CG![]() GH
GH![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】阅读材料:各类方程的解法
求解一元一次方程,根据等式的基本性质,把方程转化为x=a的形式.求解二元一次方程组,把它转化为一元一次方程来解;类似的,求解三元一次方程组,把它转化为解二元一次方程组.求解一元二次方程,把它转化为两个一元一次方程来解.求解分式方程,把它转化为整式方程来解,由于“去分母”可能产生增根,所以解分式方程必须检验.各类方程的解法不尽相同,但是它们有一个共同的基本数学思想![]() 转化,把未知转化为已知.
转化,把未知转化为已知.
用“转化”的数学思想,我们还可以解一些新的方程.例如,一元三次方程x3+x2-2x=0,可以通过因式分解把它转化为x(x2+x-2)=0,解方程x=0和x2+x-2=0,可得方程x3+x2-2x=0的解.
(1)问题:方程x3+x2-2x=0的解是x1=0,x2= ,x3= ;
(2)拓展:用“转化”思想求方程![]() 的解;
的解;
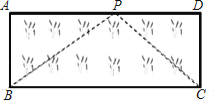
(3)应用:如图,已知矩形草坪ABCD的长AD=8m,宽AB=3m,小华把一根长为10m的绳子的一端固定在点B,沿草坪边沿BA,AD走到点P处,把长绳PB段拉直并固定在点P,然后沿草坪边沿PD、DC走到点C处,把长绳剩下的一段拉直,长绳的另一端恰好落在点C.求AP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,∠B+∠ACB=30°,AB=4,△ABC逆时针旋转一定角度后与△ADE重合,且点C恰好成为AD中点,如图
(1)指出旋转中心,并求出旋转角的度数.
(2)求出∠BAE的度数和AE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
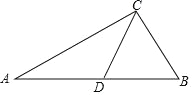
【题目】如图,在△ABC中,CD是边AB上的中线,∠B是锐角,sinB=![]() ,tanA=
,tanA=![]() ,AC=
,AC=![]() ,
,
(1)求∠B 的度数和 AB 的长.
(2)求 tan∠CDB 的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程![]() 有实数根.
有实数根.
(1)求m的值;
(2)先作![]() 的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.
的图象关于x轴的对称图形,然后将所作图形向左平移3个单位长度,再向上平移2个单位长度,写出变化后图象的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
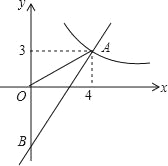
【题目】如图,一次函数y=kx+b的图象分别与反比例函数y=![]() 的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
的图象在第一象限交于点A(4,3),与y轴的负半轴交于点B,且OA=OB.
(1)求函数y=kx+b和y=![]() 的表达式;
的表达式;
(2)已知点C(0,5),试在该一次函数图象上确定一点M,使得MB=MC,求此时点M的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
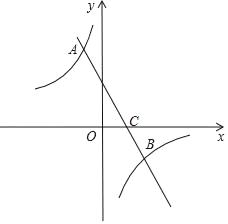
【题目】如图,直线y=kx+b(k≠0)与双曲线y=![]() (m≠0)交于点A(﹣
(m≠0)交于点A(﹣![]() ,2),B(n,﹣1).
,2),B(n,﹣1).
(1)求直线与双曲线的解析式.
(2)点P在x轴上,如果S△ABP=3,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+2ax+3a2+3(其中x是自变量),当x≥2时,y随x的增大而增大,且-2≤x≤1时,y的最大值为9,则a的值为![]()
![]()
A. 1或![]() B. -
B. -![]() 或
或![]() C.
C. ![]() D. 1
D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
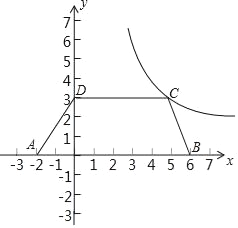
【题目】如图,在四边形ABCD中,CD∥AB,AD=BC.已知A(﹣2,0),B(6,0),D(0,3),函数y=![]() (x>0)的图象G经过点C.
(x>0)的图象G经过点C.
(1)求点C的坐标和函数y=![]() (x>0)的表达式;
(x>0)的表达式;
(2)将四边形ABCD向上平移2个单位得到四边形A'B'C'D',问点B'是否落在图象G上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com