
 已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是(11,$\sqrt{3}$).
已知,正六边形ABCDEF在直角坐标系的位置如图所示,A(-2,0),点B在原点,把正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,经过5次翻转之后,点B的坐标是(11,$\sqrt{3}$). 分析 根据正六边形的性质,求出5次翻转前进的距离=2×5=10,过点B作BG⊥x于G,求出∠BAG=60°,然后求出AG、BG,再求出OG,然后写出点B的坐标即可.
解答  解:∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,A(-2,0),
解:∵正六边形ABCDEF沿x轴正半轴作无滑动的连续翻转,每次翻转60°,A(-2,0),
∴AB=2,
∴翻转前进的距离=2×5=10,
如图,过点B作BG⊥x于G,则∠BAG=60°,
∴AG=2×$\frac{1}{2}$=1,BG=2×$\frac{\sqrt{3}}{2}$=$\sqrt{3}$,
∴OG=10+1=11,
∴点B的坐标为(11,$\sqrt{3}$).
故答案为:(11,$\sqrt{3}$).
点评 本题考查了坐标与图形变化-旋转,正六边形的性质,确定出最后点B所在的位置是解题的关键,难点在于作辅助线构造出直角三角形.


科目:初中数学 来源: 题型:填空题
 如图,点E是正方形ABCD内一点,点E到点A,B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$.将△ADE绕点A旋转至△ABG,连结ABG,连结AE,并延长AE与BC相交于点F,连接GF,则线段GF长为$\frac{\sqrt{178}}{3}$.
如图,点E是正方形ABCD内一点,点E到点A,B和D的距离分别为1,2$\sqrt{2}$,$\sqrt{10}$.将△ADE绕点A旋转至△ABG,连结ABG,连结AE,并延长AE与BC相交于点F,连接GF,则线段GF长为$\frac{\sqrt{178}}{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
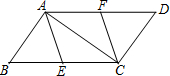 已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.
已知,如图,在?ABCD中,AC是对角线,AB=AC,点E、F分别是BC、AD的中点,连接AE,CF.查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 字母A | B. | 字母B | C. | 字母D | D. | 字母F |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算CD,CE的长,并标明限制高度.
为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下停车库的设计示意图,其中,AB⊥BD,∠BAD=18°,C在BD上,BC=0.5m.按规定,地下停车库坡道口上方要张贴限高标志,以便告知停车人车辆能否安全驶入,请你根据该图计算CD,CE的长,并标明限制高度.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,树AB垂直于地面,为测树高,小明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助小明计算出树的高度吗?
如图,树AB垂直于地面,为测树高,小明在C处,测得∠ACB=15°,他沿CB方向走了20米,到达D处,测得∠ADB=30°,你能帮助小明计算出树的高度吗?查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com