
| AE |
| AD |
| m |
| n |
| 1 |
| 2 |
| BE |
| AG |
| m |
| n |
| n |
| m |
| n |
| m |
| n |
| m |
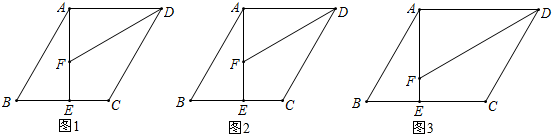
 解:(1)CD=AF+BE,
解:(1)CD=AF+BE,| 1 |
| 2 |
| 1 |
| 2 |
|
| 1 |
| 2 |
|
| m |
| n |
| BE |
| AG |
| m |
| n |
| BE |
| AG |
| AE |
| AD |
| m |
| n |
| AB |
| DG |
| m |
| n |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| n |
| m |
| m |
| n |


科目:初中数学 来源: 题型:
 如图,开发区为提高某段海堤的防潮能力,将长1000m的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m,将原来的背水坡度AD(坡比1:1)改成现在的背水坡(坡比1:2),已知AD=8.0m,求完成这一工程所需的土方.
如图,开发区为提高某段海堤的防潮能力,将长1000m的一堤段(原海堤的横断面如图中的梯形ABCD)的堤面加宽1.6m,将原来的背水坡度AD(坡比1:1)改成现在的背水坡(坡比1:2),已知AD=8.0m,求完成这一工程所需的土方.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
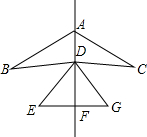 如图是一个风筝的图案,它是以直线为对称轴的轴对称图形,下列结论中不一定成立的是( )
如图是一个风筝的图案,它是以直线为对称轴的轴对称图形,下列结论中不一定成立的是( )| A、△ABD≌△ACD |
| B、AF垂直平分EG |
| C、直线BG,CE的交点在AF上 |
| D、△DEG是等边三角形 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,AC平分∠BCD,AB=AD,AE⊥BC于点E,AF⊥CD于点F.
如图,AC平分∠BCD,AB=AD,AE⊥BC于点E,AF⊥CD于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com