
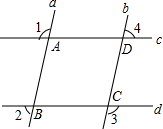
 如图,直线c,d与直线a,b相交于点A,B,C,D,∠1=∠3,∠2=∠4.求证:AB=CD.
如图,直线c,d与直线a,b相交于点A,B,C,D,∠1=∠3,∠2=∠4.求证:AB=CD.  阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:选择题
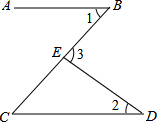 如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )
如图,直线AB、CD被BC所截,若AB∥CD,∠1=45°,∠2=35°,则∠3的大小是( )| A. | 80° | B. | 70° | C. | 90° | D. | 100° |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
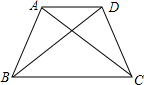 如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )
如图,梯形ABCD中,AD∥BC,AB=CD,AC⊥BD,AD=3,BC=5,则梯形ABCD的高是( )| A. | $4\sqrt{2}$ | B. | 4 | C. | $2\sqrt{2}$ | D. | 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1 | B. | -1 | C. | 2 | D. | -2 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
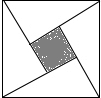 如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是$\frac{1}{9}$,则大、小两个正方形的边长之比是3:1.
如图,“赵爽弦图”是由四个全等的直角三角形与中间一个小正方形拼成的一个大正方形,随机在大正方形及其内部区域投针,若针扎到小正方形(阴影部分)的概率是$\frac{1}{9}$,则大、小两个正方形的边长之比是3:1.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com