我校八年级共有1300名学生，准备调查他们对“低碳”知识的了解程度．
(1) 在确定调查方式时，团委设计了以下三种方案：
方案一：调查八年级部分女生；
方案二：调查八年级部分男生；
方案三：到八年级每个班去随机调查一定数量的学生．
请问其中最具有代表性的一个方案是______________；
(2) 团委采用了最具有代表性的调查方案，并用收集到的数据绘制出两幅不完整的统计图(如图①、图②所示)，请你根据图中信息，将两个统计图补充完整；
(3) 请你估计我校八年级约有多少名学生比较了解“低碳”知识。
天天向上一本好卷系列答案
小学生10分钟应用题系列答案科目：初中数学 来源： 题型：
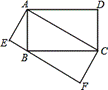
如图，四边形ABCD和四边形AEFC是两个矩形，点B在EF边上，若矩形ABCD和矩形AEFC的面积分别是S1、S2
的大小关系是____________.
 |
查看答案和解析>>
科目：初中数学 来源： 题型：
已知四边形OABC、四边形OADE、四边形OFGH都是正方形。
(1) 如图①，正方形OFGH的顶点F、H分别在边OA、OC上，连接AH、CF、EF，点M 为CF的中点，连接OM，则线段AH与OM之间的数量关系是_____, 位置关系是______.
如图②，将图①中的正方形OFGH绕点O顺时针旋转，旋转角为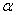
(
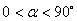)，其它条件不变，判断(1)中的两个结论是否仍然成立，若成立，请证明；若不成立，请说明理由．
(2) 
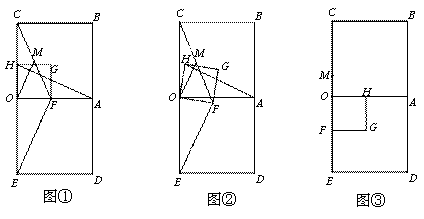如图③，将将图①中的正方形OFGH绕点O顺时针旋转90º，使得点H落在边OA上，点F落在边OE上，点M为线段CF的中点，请你判断线段AH与OM之间的数量关系是否发生变化，写出你的猜想，并加以证明．
查看答案和解析>>
科目：初中数学 来源： 题型：
某次器乐比赛设置了7个获奖名额，共有11名选手参加，他们的比赛得分均不相同．若知道某位选手的得分.要判断他能否获奖，在下列11名选手成绩的统计量中，只需知道 【 】A．方差 B．平均数
C．众数 D．中位数
查看答案和解析>>
科目：初中数学 来源： 题型：
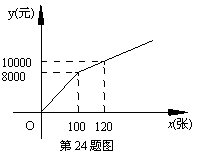
为丰富群众的业余生活，我市准备组织篮球比赛，市体育局策划本次活动，在与单位协商团购票时推出两种方案．设购买门票数为x（张），总费用为y（元）．方案一：若单位赞助广告费8000元，则该单位所购门票的价格为每张50元；（总费用＝广告赞助费+门票费）
方案二：直接购买门票方式如图所示．解答下列问题：
（1）方案一中，y与x的函数关系式为 ；
方案二中，当0≤x≤100时，y与x的函数关系式为 ，
当x＞100时，y与x的函数关系式为 ；
（2）如果购买本场篮球赛门票超过100张，你将选择哪一种方案，使总费用最省？请说明理由；
 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
（1）（本题1分）三
无意义．