
【题目】在△ABC中,∠A=60°,∠ABC=45°,AB=4![]() ,点D为AC上一动点,以BD为直径的⊙O交BC于点E,交AB于点F,则EF的最小值是______.
,点D为AC上一动点,以BD为直径的⊙O交BC于点E,交AB于点F,则EF的最小值是______.
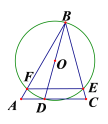
【答案】3![]()
【解析】
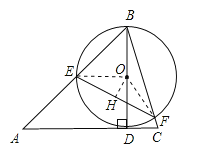
由垂线段的性质可知,当BD为△ABC的边AC上的高时,直径BD最短,此时线段EF=2EH=2OEsin∠EOH=2OEsin45°,因此当半径OE最短时,EF最短,连接OE,OF,过O点作OH⊥EF,垂足为H,在Rt△ADB中,解直角三角形求直径BD,由圆周角定理可知∠EOH=![]() ∠EOF=∠ABC=45°,在Rt△EOH中,解直角三角形求EH,由垂径定理可知EF=2EH.
∠EOF=∠ABC=45°,在Rt△EOH中,解直角三角形求EH,由垂径定理可知EF=2EH.
由垂线段的性质可知,当BD为△ABC的边BC上的高时,直径BD最短,
如图,
 ,
,
连接OE,OF,过O点作OH⊥EF,垂足为H,
∵在Rt△ADB中,∠BAC=60°,AB=4![]() ,
,
∴BD=6,即此时圆的直径为6,
由圆周角定理可知∠EOH=![]() ∠EOF=∠ABC=45°,
∠EOF=∠ABC=45°,
∴在Rt△EOH中,EH=OEsin∠EOH=3×![]() =
=![]() ,
,
由垂径定理可知EF=2EH=3![]() .
.
故答案为:3![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,已知![]() 为
为![]() 的直径,
的直径,![]() 、
、![]() 是
是![]() 的弦,
的弦,![]() 是
是![]() 的切线,切点为
的切线,切点为![]() ,
,![]() ,
,![]() 、
、![]() 的延长线相交于点
的延长线相交于点![]() .
.
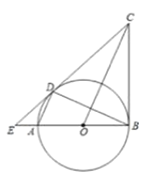
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求
,求![]() 的半径.
的半径.
(3)在(2)中的条件下,![]() ,将
,将![]() 以点
以点![]() 为中心逆时针旋转
为中心逆时针旋转![]() ,求
,求![]() 扫过的图形的面积(结果用
扫过的图形的面积(结果用![]() 表示).
表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,B是![]() 的半径OA上的一点(不与端点重合),过点B作OA的垂线交
的半径OA上的一点(不与端点重合),过点B作OA的垂线交![]() 于点C,D,连接OD,E是
于点C,D,连接OD,E是![]() 上一点,
上一点,![]() ,过点C作
,过点C作![]() 的切线l,连接OE并延长交直线l于点F.
的切线l,连接OE并延长交直线l于点F.
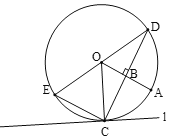
(1)①依题意补全图形.
②求证:∠OFC=∠ODC.
(2)连接FB,若B是OA的中点,![]() 的半径是4,求FB的长.
的半径是4,求FB的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某地质量监管部门对辖区内的甲、乙两家企业生产的某同类产品进行检查,分别随机抽取了50件产品并对某一项关键质量指标做检测,获得了它们的质量指标值s,并对样本数据(质量指标值s)进行了整理、描述和分析.下面给出了部分信息.
a.该质量指标值对应的产品等级如下:
质量指标值 |
|
|
|
|
|
等级 | 次品 | 二等品 | 一等品 | 二等品 | 次品 |
说明:等级是一等品,二等品为质量合格(其中等级是一等品为质量优秀).
等级是次品为质量不合格.
b.甲企业样本数据的频数分布统计表如下(不完整).
c.乙企业样本数据的频数分布直方图如下.
甲企业样本数据的频数分布表
分组 | 频数 | 频率 |
| 2 | 0.04 |
| m | |
| 32 | n |
| 0.12 | |
| 0 | 0.00 |
合计 | 50 | 1.00 |
乙企业样本数据的频数分布直方图
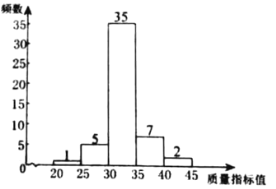
d.两企业样本数据的平均数、中位数、众数、极差、方差如下:
平均数 | 中位数 | 众数 | 极差 | 方差 | |
甲企业 | 31.92 | 32.5 | 34 | 15 | 11.87 |
乙企业 | 31.92 | 31.5 | 31 | 20 | 15.34 |
根据以上信息,回答下列问题:
(1)m的值为________,n的值为________.
(2)若从甲企业生产的产品中任取一件,估计该产品质量合格的概率为________;若乙企业生产的某批产品共5万件,估计质量优秀的有________万件;
(3)根据图表数据,你认为________企业生产的产品质量较好,理由为______________.(从某个角度说明推断的合理性)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:
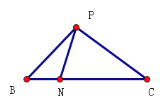
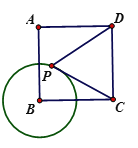
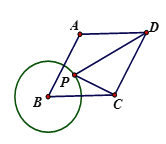
图1 图2 图3
(1)初步思考:
如图1, 在![]() 中,已知
中,已知![]() ,BC=4,N为BC上一点且
,BC=4,N为BC上一点且![]() ,试说明:
,试说明:![]()
(2)问题提出:
如图2,已知正方形ABCD的边长为4,圆B的半径为2,点P是圆B上的一个动点,求![]() 的最小值.
的最小值.
(3)推广运用:
如图3,已知菱形ABCD的边长为4,∠B﹦60°,圆B的半径为2,点P是圆B上的一个动点,求![]() 的最大值.
的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AB为⊙O的直径.
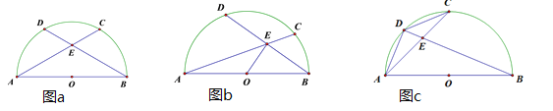
(1)如图a,点D为![]() 的中点,当弦BD=AC时,求∠A.
的中点,当弦BD=AC时,求∠A.
(2)如图b,点D为![]() 的中点,当AB=6,点E为BD的中点时,求OE的长.
的中点,当AB=6,点E为BD的中点时,求OE的长.
(3)如图c,点D为![]() 上任意一点(不与A、C重合),若点C为
上任意一点(不与A、C重合),若点C为![]() 的中点,探求BD、AD、CD之间的数量关系,直接写出你探求的结论,不要求证明.
的中点,探求BD、AD、CD之间的数量关系,直接写出你探求的结论,不要求证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(12分)如图,在Rt△ABC中,∠ACB=90°,AC=8,BC=6,CD⊥AB于点D.点P从点D出发,沿线段DC向点C运动,点Q从点C出发,沿线段CA向点A运动,两点同时出发,速度都为每秒1个单位长度,当点P运动到C时,两点都停止.设运动时间为t秒.
(1)求线段CD的长;
(2)设△CPQ的面积为S,求S与t之间的函数关系式,并确定在运动过程中是否存在某一时刻t,使得S△CPQ∶S△ABC=9∶100?若存在,求出t的值;若不存在,说明理由;
(3)当t为何值时,△CPQ为等腰三角形?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,公园中一正方形水池中有一喷泉,喷出的水流呈抛物线状,测得喷出口高出水面0.8m,水流在离喷出口的水平距离1.25m处达到最高,密集的水滴在水面上形成了一个半径为3m的圆,考虑到出水口过高影响美观,水滴落水形成的圆半径过大容易造成水滴外溅到池外,现决定通过降低出水口的高度,使落水形成的圆半径为2.75m,则应把出水口的高度调节为高出水面( )
A.0.55米B.![]() 米C.
米C.![]() 米D.0.4米
米D.0.4米
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】商场销售服装,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价
元,为扩大销售量,减少库存,该商场决定采取适当的降价措施,经调查发现,一件衣服降价![]() 元,每天可多售出
元,每天可多售出![]() 件.
件.
![]() 设每件降价
设每件降价![]() 元,每天盈利
元,每天盈利![]() 元,请写出
元,请写出![]() 与
与![]() 之间的函数关系式;
之间的函数关系式;![]() 若商场每天要盈利
若商场每天要盈利![]() 元,同时尽量减少库存,每件应降价多少元?
元,同时尽量减少库存,每件应降价多少元?
![]() 每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
每件降价多少元时,商场每天盈利达到最大?最大盈利是多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com