
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.

科目:初中数学 来源: 题型:
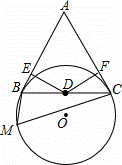
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
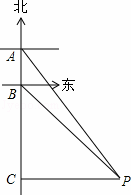
有一轮船在A处测得南偏东30°方向上有一小岛P,轮船沿正南方向航行至B处,测得小岛P在南偏东45°方向上,按原方向再航行10海里至C处,测得小岛P在正东方向上,则A,B之间的距离是( )海里.
A. 10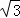 B. 10
B. 10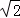 ﹣10 C. 10 D. 10
﹣10 C. 10 D. 10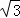 ﹣10
﹣10
查看答案和解析>>
科目:初中数学 来源: 题型:
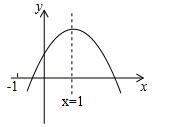
已知二次函数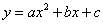 的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,
的图象如图所示,有以下结论:①abc>0,②a﹣b+c<0,③2a=b,④4a+2b+c>0,⑤若点(﹣2,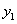 )和(
)和( ,
,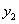 )在该
)在该 图象上,则
图象上,则 .其中正确的
.其中正确的 结论是 (填入正确结论的序号).
结论是 (填入正确结论的序号).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com