
如图,已知BC是⊙O的弦,A是⊙O外一点,△ABC为正三角形,D为BC的中点,M为⊙O上一点,并且∠BMC=60°.
(1)求证:AB是⊙O的切线;
(2)若E,F分别是边AB,AC上的两个动点,且∠EDF=120°,⊙O的半径为2,试问BE+CF的值是否为定值?若是,求出这个定值;若不是,请说明理由.
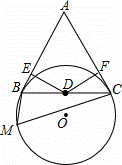
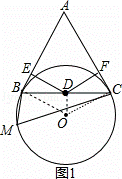
(1)证明:连结OB、OD,如图1,
∵D为BC的中点,
∴OD⊥BC,∠BOD=∠COD,
∴∠ODB=90°,
∵∠BMC=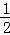 ∠BOC,
∠BOC,
∴∠BOD=∠M=60°,
∴∠OBD=30°,
∵△ABC为正三角形,
∴∠ABC=60°,
∴∠ABO=60°+30°=90°,
∴AB⊥OB,
∴AB是⊙O的切线;
(2)解:BE+CF的值是为定值.
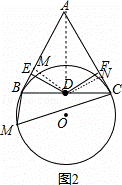
作DM⊥AB于M,DN⊥AC于N,连结AD,如图2,
∵△ABC为正三角形,D为BC的中点,
∴AD平分∠BAC,∠BAC=60°,
∴DM=DN,∠MDN=120°,
∵∠EDF=120°,
∴∠MDE=∠NDF,
在△DME和△DNF中,
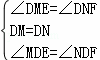 ,
,
∴△DME≌△DNF,
∴ME=NF,
∴BE+CF=BM﹣EM+CN+NF=BM+CN,
在Rt△DMB中,∵∠DBM=60°,
∴BM=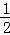 BD,
BD,
同理可得CN=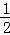 OC,
OC,
∴BE+CF=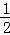 OB+
OB+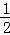 OC=
OC=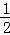 BC,
BC,
∴BE+CF的值是定值,为等边△ABC边长的一半.


 习题精选系列答案
习题精选系列答案科目:初中数学 来源: 题型:
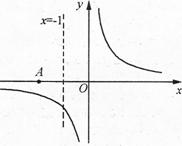
已知点A(-2,0),B为直线x=-1上一个动点,P为直线AB与双曲线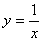 的交点,且AP=2AB,则满足条件的点P的个数是( )
的交点,且AP=2AB,则满足条件的点P的个数是( )
A.0个 B.1个 C.2个 D.3个
查看答案和解析>>
科目:初中数学 来源: 题型:
由大小两种货车,3辆大车与4辆小车一次可以运货22吨,2辆大车与6辆小车一次可以运货23吨.请根据以上信息,提出一个能用方程(组)解决的问题,并写出这个问题的解答过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在五边形ABCDE中,AB=AC=AD=AE,且AB∥ED,∠EAB=120°,则∠DCB=( )
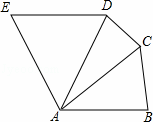
A.150° B. 160° C. 130° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
如图,在△ABC中,∠B=60°,⊙O是△ABC的外接圆,过点A作⊙O的切线,交CO的延长线于点M,CM交⊙O于点D.
(1)求证:AM=AC;
(2)若AC=3,求MC的长.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com