
【题目】如图,等边△ABC中,点D在AC上(CD<![]() AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
AC),连接BD.操作:以A为圆心,AD长为半径画弧,交BD于点E,连接AE.
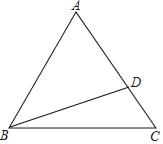
(1)请补全图形,探究∠BAE、∠CBD之间的数量关系,并证明你的结论;
(2)把BD绕点D顺时针旋转60°,交AE于点F,若EF=mAF,求![]() 的值(用含m的式子表示).
的值(用含m的式子表示).
【答案】(1)图形见解析,∠BAE=2∠CBD,理由见解析;(2)![]()
![]() ,理由见解析
,理由见解析
【解析】
(1)根据圆周角和圆心角的关系得:2∠BDH=∠BAE,由等腰三角形的性质得HD∥BC,由平行线的性质可得结论;
(2)如图2,作辅助线,由旋转得:△BDM是等边三角形,证明△AMB≌△CDB(SAS),得AM=CD,∠MAB=∠C=60°,证明△ABD∽△DFE,设AF=a,列比例式可得结论
(1)如图1,∠BAE=2∠CBD.
设弧DE与AB交于H,连接DH,
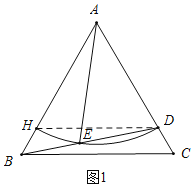
∴2∠BDH=∠BAE,
又∵AD=AH,AB=AC,∠BAC=60°,
∴∠AHD=∠ADH=60°,∠ABC=∠C=60°,
∴∠AHD=∠ABC,
∴HD∥BC,
∴∠DBC=∠HDB,
∴∠BAE=2∠DBC;
(2)如图2,连接AM,BM,
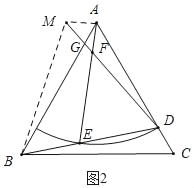
由旋转得:BD=DM,∠BDM=60°,
∴△BDM是等边三角形,
∴BM=BD,∠MBD=60°,
∵∠ABM+∠ABD=∠ABD+∠CBD,
∴∠ABM=∠CBD,
∵△ABC是等边三角形,
∴AB=AC,
∴△AMB≌△CDB(SAS),
∴AM=CD,∠MAB=∠C=60°,
∵∠AGM=∠BGD,∠MAB=∠BDM=60°,
∴∠AMD=∠ABD,
由(1)知:AD=AE,
∴∠AED=∠ADE,
∵∠EDF=∠BAD,
∴△ABD∽△DFE,
∴∠EFD=∠ABD=∠AFM=∠AMD,
∴AF=AM=CD,
设AF=a,则EF=ma,AE=a+ma=(m+1)a,
∴AB=AD+CD=AE+CD=(m+2)a,
由△ABD∽△DFE,
∴![]() =
=![]() =
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,在由边长为1个单位长度的小正方形组成的网格图中,△ABC的顶点都在网格线交点上.
(1)图中AC边上的高为 个单位长度;
(2)只用没有刻度的直尺,在所给网格图中按如下要求画图(保留必要痕迹):
①以点C为位似中心,把△ABC按相似比1:2缩小,得到△DEC;
②以AB为一边,作矩形ABMN,使得它的面积恰好为△ABC的面积的2倍.
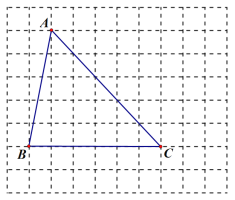
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】5G网络是第五代移动通信网络,它将推动我国数字经济发展迈上新台阶. 据预测,2020年到2030年中国5G直接经济产出和间接经济产出的情况如下图所示.
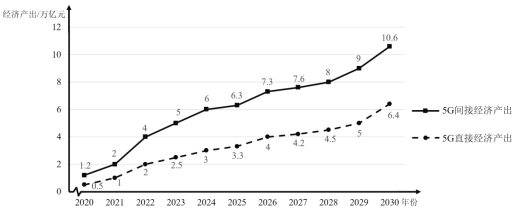
根据上图提供的信息,下列推断不合理的是( )
A.2030年5G间接经济产出比5G直接经济产出多4.2万亿元
B.2020年到2030年,5G直接经济产出和5G间接经济产出都是逐年增长
C.2030年5G直接经济产出约为2020年5G直接经济产出的13倍
D.2022年到2023年与2023年到2024年5G间接经济产出的增长率相同
查看答案和解析>>
科目:初中数学 来源: 题型:
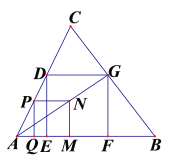
【题目】如图,正方形PQMN在△ABC内,点P在AC上,点Q、M在AB上,N在△ABC内,连接AN并延长交BC于G,过G点作GD∥AB交AC于D,过D、G分别作DE ⊥AB,GF⊥AB,垂足分别为E、F.
(1)求证:DG=GF;
(2)若AB=10,S△ABC=40,试求四边形DEFG的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在![]() 中,
中,![]() 是
是![]() 的直径,
的直径,![]() 交
交![]() 于点
于点![]() ,过点
,过点![]() 的直线交
的直线交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,试求
,试求![]() 的长;
的长;
(3)如图2,点![]() 是弧
是弧![]() 的中点,连结
的中点,连结![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的值.
的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校组织甲、乙两班学生参加“美化校园”的义务劳动.如果甲班做2小时,乙班做3小时,那么可完成全部工作的一半;如果甲班先做2小时后另有任务,剩下工作由乙班单独完成,那么乙班所用的时间恰好比甲班单独完成全部工作的时间多1小时.问:甲乙两班单独完成这项工作各需多少时间?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某工艺厂设计了款成本为![]() 元件的工艺品投放市场进行试销,经过调查,得到如下数据:
元件的工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价 | ··· |
|
|
|
| ··· |
每天销售量 | ··· |
|
|
|
| ··· |
(1)若![]() 是
是![]() 的一次函数,求出此函数的关系式:
的一次函数,求出此函数的关系式:
(2)若用![]() (元)表示工艺厂试销该工艺品每天获得的利润,试求
(元)表示工艺厂试销该工艺品每天获得的利润,试求![]() (元)与
(元)与![]() (元/件)之间的函数关系式.
(元/件)之间的函数关系式.
(3)若该工艺品的每天的总成木不能超过![]() 元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
元,那么销售单价定为多少元时,工艺厂试销工艺品每天获得的利润最大,最大是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
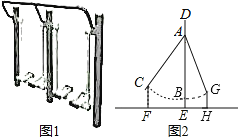
【题目】如图1是小区常见的漫步机,当人踩在踏板上,握住扶手,像走路一样抬腿,就会带动踏板连杆绕轴旋转.如图2,从侧面看,踏板静止DE上的线段AB重合,测得BE长为0.21m,当踏板连杆绕着A旋转到AC处时,测得∠CAB=42°,点C到地面的距离CF长为0.52m,当踏板连杆绕着点A旋转到AG处∠GAB=30°时,求点G距离地面的高度GH的长.(精确到0.1m,参考数据:sin42°≈0.67,cos42°≈0.74,tan42°≈0.90,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】春季正是新鲜草莓上市的季节,甲、乙两家水果店,平时以同样的价格出售品质相同的草莓,“草莓节”期间,甲、乙两家商店都让利酬宾,顾客的折后付款金额![]() 、
、![]() (单位:元)与标价应付款金额x(单位:元)之间的函数关系如图所示.
(单位:元)与标价应付款金额x(单位:元)之间的函数关系如图所示.
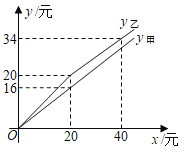
(1)求![]() 、
、![]() 关于x的函数关系式;
关于x的函数关系式;
(2)“草莓节”期间,如何选择甲、乙两家水果店购买草莓更省钱?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com