
【题目】已知关于x的方程![]()
(1)若方程有两个相等的实数根,求m的值,并求出此时方程的根;
(2)是否存在正数m,使方程的两个实数根的平方和等于224.若存在,求出满足条件的m的值;若不存在,请说明理由.
【答案】(1)x1=x2=﹣2.(2)不存在正数m使方程的两个实数根的平方和等于224
【解析】
(1)方程有两相等的实数根,利用△=0求出m的值.化简原方程求得方程的根.
(2)利用根与系数的关系x1+x2=-![]() , =4m-8,x1x2=
, =4m-8,x1x2=![]() =4m2,x12+x22=(x1+x2)2-2x1x2,代入即可得到关于m的方程,求出m的值,再根据△来判断所求的m的值是否满足原方程.
=4m2,x12+x22=(x1+x2)2-2x1x2,代入即可得到关于m的方程,求出m的值,再根据△来判断所求的m的值是否满足原方程.
(1)∵a=![]() ,b=﹣(m﹣2),c=m2方程有两个相等的实数根,
,b=﹣(m﹣2),c=m2方程有两个相等的实数根,
∴△=0,即△=b2﹣4ac=[﹣(m﹣2)]2﹣4×![]() ×m2=﹣4m+4=0,
×m2=﹣4m+4=0,
∴m=1.
原方程化为:![]() x2+x+1=0 x2+4x+4=0,(x+2)2=0,
x2+x+1=0 x2+4x+4=0,(x+2)2=0,
∴x1=x2=﹣2.
(2)不存在正数m使方程的两个实数根的平方和等于224.
∵x1+x2=﹣![]() =4m﹣8,x1x2=
=4m﹣8,x1x2=![]() =4m2x12+x22=(x1+x2)2﹣2x1x2=(4m﹣8)2﹣2×4m2=8m2﹣64m+64=224,
=4m2x12+x22=(x1+x2)2﹣2x1x2=(4m﹣8)2﹣2×4m2=8m2﹣64m+64=224,
即:8m2﹣64m﹣160=0,
解得:m1=10,m2=﹣2(不合题意,舍去),
又∵m1=10时,△=﹣4m+4=﹣36<0,此时方程无实数根,
∴不存在正数m使方程的两个实数根的平方和等于224.


科目:初中数学 来源: 题型:
【题目】为弘扬中华民族传统文化,某校举办了“燕城诗文大赛”活动,从中随机抽取部分学生的比赛成绩,根据成绩(成绩都高于50分),绘制了如下的统计图表(不完整):
组别 | 分数 | 人数 |
第1组 |
| 16 |
第2组 |
|
|
第3组 |
| 20 |
第4组 |
|
|
第5组 |
| 6 |
请根据以上信息,解答下列问题:
(1)此次随机抽取的学生数是 人,![]() ,
,![]() ;
;
(2)计算扇形统计图中“第5组”所在扇形圆心角的度数;
(3)若该校共有1500名学生,那么成绩低于70分的约有多少人?

查看答案和解析>>
科目:初中数学 来源: 题型:
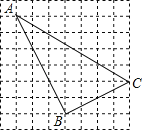
【题目】已知图中的每个方格都是边长为1的小正方形,每个小正方形的顶点称为格点,△ABC的顶点在格点上,称为格点三角形,请按要求完成下列各题
(1)填空:
AB= ,BC= ,AC= ;
(2)试判断△ABC的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
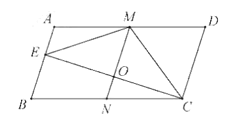
【题目】如图,平行四边形ABCD中,![]() 于点E,CE的垂真平分线MV分别交AD、BC于M、N,交CE于O,连接CM、EM,下列结论:(1)
于点E,CE的垂真平分线MV分别交AD、BC于M、N,交CE于O,连接CM、EM,下列结论:(1)![]() (2)
(2)![]() (3)
(3)![]() (4)
(4)![]() ·其中正确的个数有( )
·其中正确的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】银川九中要举办“不忘初心跟党走”2018年元旦合唱比赛,为迎接比赛,某校区七年级(3)(4)班决定订购同一套服装,两班一共有103人(三班人数多于四班),经协商,某服装店给出的价格如下:
购买人数/人 | 1~50人 | 50~100人 | 100以上人 |
每套服装价格/元 | 50 | 45 | 40 |
(1)如果两个班都以班为单位分别购买,则一共需花费4875元,那么三、四班各有多少名学生?
(2)如果两个班联合起来,做为一个整体购买,则能节省多少元钱?
(3)该服装店此次出售的服装每套成本是32元,如果按上面的第(2)问形式购买,请计算这个服装店此次出售服装的利润率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年4月23日,是第23个世界读书日.为了推进中华传统文化教育,营造浓厚的读书氛围,我市某学校举办了“让读书成为习惯,让书香溢病校园”主题活动.为了解学生每周阅读时间,该校随机抽取了部分学生进行调查,根据调查结果,将阅诙时间![]() (单位:小时)分成了
(单位:小时)分成了![]() 组,
组, ![]()
![]()
![]() ,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
,下图是根据这组数据绘制的两幅不完整的统计图.请你结合图中所给信息解答下列问题:
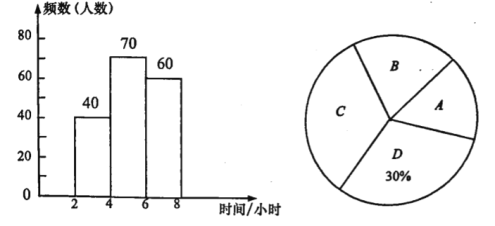
(1)这次随机抽取了 名学生进行调查;
(2)补全频数分布直方图;
(3)计算扇形统计图中扇形![]() 的圆心角的度数;
的圆心角的度数;
(4)若该校共有![]() 名学生,请你估计每周阅读时间不足
名学生,请你估计每周阅读时间不足![]() 小时的学生共有多少名?
小时的学生共有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】节约是中华民族的传统美德.为倡导市民节约用水的意识,某市对市民用水实行“阶梯收费”,制定了如下用水收费标准:每户每月的用水不超过![]() 立方米时,水价为每立方米
立方米时,水价为每立方米![]() 元,超过
元,超过![]() 立方米时,超过的部分按每立方米
立方米时,超过的部分按每立方米![]() 元收费.
元收费.
(1)该市某户居民9月份用水![]() 立方米(
立方米(![]() ),应交水费
),应交水费![]() 元,请你用含
元,请你用含![]() 的代数式表示
的代数式表示![]() ;
;
(2)如果某户居民12月份交水费![]() 元,那么这个月该户居民用了多少立方米水?
元,那么这个月该户居民用了多少立方米水?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】快车以200km/h的速度由甲地开往乙地再返回甲地,慢车以75km/h的速度同时从乙地出发开往甲地,已知快车回到甲地时,慢车距离甲地还有225km,则
(1)甲乙两地相距多少千米?
(2)从出发开始,经过多长时间两车相遇?
(3)几小时后两车相距100千米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com