
【题目】(10分)一块直角三角形木版的一条直角边AB为3m,面积为6![]() ,要把它加工成一个面积最大的正方形桌面,小明打算按图①进行加工,小华准备按图②进行裁料,他们谁的加工方案符合要求?
,要把它加工成一个面积最大的正方形桌面,小明打算按图①进行加工,小华准备按图②进行裁料,他们谁的加工方案符合要求?

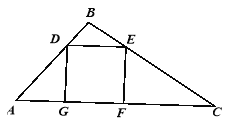
图① 图②
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD中,AC⊥BD于点O,AO=CO=8,BO=DO=6,点P为线段AC上的一个动点。

⑴ 填空:AD=CD=_____ .
⑵ 过点P分别作PM⊥AD于M点,作PH⊥DC于H点.连结PB,在点P运动过程中,PM+PH+PB的最小值为____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与x轴交于点A,与y轴交于点B.
的图象与x轴交于点A,与y轴交于点B.
(1)求A、B两点的坐标.
(2)求△AOB的面积.
(3)若点C在直线AB上,且S△BOC=2,求点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某水果店以4元/千克的价格购进一批水果,由于销售状况良好,该店又再次购进同一种水果,第二次进货价格比第一次每千克便宜了0.5元,所购水果重量恰好是第一次购进水果重量的2倍,这样该水果店两次购进水果共花去了2200元.
(1)该水果店两次分别购买了多少元的水果?
(2)在销售中,尽管两次进货的价格不同,但水果店仍以相同的价格售出,若第一次购进的水果有3%的损耗,第二次购进的水果有5%的损耗,该水果店希望售完这些水果获利不低于1244元,则该水果每千克售价至少为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,平面直角坐标系中,O为原点,点A坐标为(﹣4,0),AB∥y轴,点C在y轴上,一次函数y=![]() x+3的图象经过点B、C.
x+3的图象经过点B、C.

(1)点C的坐标为_____,点B的坐标为_____;
(2)如图②,直线l经过点C,且与直线AB交于点M,O'与O关于直线l对称,连接CO'并延长,交射线AB于点D.
①求证:△CMD是等腰三角形;
②当CD=5时,求直线l的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王剪了两张直角三角形纸片,进行了如下的操作:
(1)如图1,将Rt△ABC沿某条直线折叠,使斜边的两个端点A与B重合,折痕为DE,若AC=6cm,BC=8cm,求CD的长.
(2)如图2,小王拿出另一张Rt△ABC纸片,将直角边AC沿直线AD折叠,使它落在斜边AB上,且与AE重合,若AC=6cm,BC=8cm,求CD的长
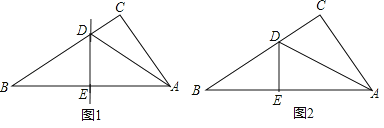
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形ABCD中,E为对角线BD上一点,过E点作EF⊥BD交BC于F,连接DF,G为DF中点,连接EG,CG.

(1)求证:EG=CG;
(2)将图①中△BEF绕B点逆时针旋转45°,如图②所示,取DF中点G,连接EG,CG.
问(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由;
(3)将图①中△BEF绕B点旋转任意角度,如图③所示,再连接相应的线段,问(1)中的结论是否仍然成立?通过观察你还能得出什么结论(均不要求证明).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在□ABCD中,E是AD的中点,延长CB到点F,使![]() ,连接BE、AF.
,连接BE、AF.
(1)完成画图并证明四边形AFBE是平行四边形;
(2)若AB=6,AD=8,∠C=60°,求BE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象交于A(1,6),B(3,n)两点.
的图象交于A(1,6),B(3,n)两点.
(1)求反比例函数和一次函数的表达式;
(2)根据图象写出不等式kx+b﹣![]() >0的解集;
>0的解集;
(3)若点M在x轴上、点N在y轴上,且以M、N、A、B为顶点的四边形是平行四边形,请直接写出点M、N的坐标.
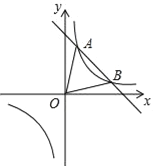
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com