
【题目】病人按规定的剂量服用某种药物,测得服药后2小时,每毫升血液中的含药量达到最大值为4毫克,已知服药后,2小时前每毫升血液中的含药量y(毫克)与时间x(小时)成正比例,2小时后y与x成反比例(如图所示).根据以上信息解答下列问题. 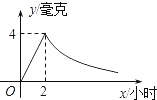
(1)求当0≤x≤2时,y与x的函数关系式;
(2)求当x>2时,y与x的函数关系式;
(3)若每毫升血液中的含药量不低于2毫克时治疗有效,则服药一次,治疗疾病的有效时间是多长?
【答案】
(1)解:根据图象,正比例函数图象经过点(2,4),
设函数解析式为y=kx,
则2k=4,
解得k=2,
所以函数关系为y=2x(0≤x≤2)
(2)解:根据图象,反比例函数图象经过点(2,4),
设函数解析式为y= ![]() ,
,
则 ![]() =4,
=4,
解得k=8,
所以,函数关系为y= ![]() (x>2)
(x>2)
(3)解:当y=2时,2x=2,解得x=1,
![]() =2,解得x=4,
=2,解得x=4,
4﹣1=3小时,
∴服药一次,治疗疾病的有效时间是3小时
【解析】(1)根据点(2,4)利用待定系数法求正比例函数解形式;(2)根据点(2,4)利用待定系数法求反比例函数解形式;(3)根据两函数解析式求出函数值是2时的自变量的值,即可求出有效时间.


 口算题天天练系列答案
口算题天天练系列答案科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD的对角线相交于点O,AE平分∠BAD交BC于E,若∠CAE=15°,则∠AEO=( )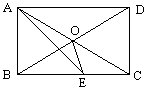
A.30°
B.25°
C.22.5°
D.20
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探索与推断:
(1)有四个数,把其中每三个数相加,其和分别为22,24,27,20.求这四个数分别为多少?
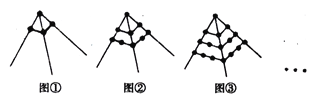
(2)观察下列图形中的点的个数,若按其规律再画下去:
①请你画出第4个图形,并指出第4个图形中的点的个数;
②第n个图形中所有点的个数是多少?(用含n的代数式表示)
③若图形中共有1600个点,则该图是第几个图形?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的面积为4,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一点P,使PD+PE的和最小,则这个最小值为( )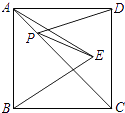
A.![]()
B.3
C.4
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
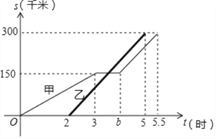
【题目】甲、乙两辆汽车沿同一路线从A地前往B地,甲以a千米/时的速度匀速行驶,途中出现故障后停车维修,修好后以2a千米/时的速度继续行驶;乙在甲出发2小时后匀速前往B地,设甲、乙两车与A地的路程为s(千米),甲车离开A地的时间为t(时),s与t之间的函数图象如图所示.
(1)求a和b的值.
(2)求两车在途中相遇时t的值.
(3)当两车相距60千米时,t= 时.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com