
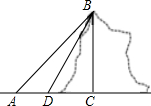
 如图,小明在A处用测角仪观测一座山的山顶B的仰角为45°,然后他前进了50米到达D处,观测B处的仰角为60°,求小山的高度BC(结果要求精确到1米,参考数据:$\sqrt{3}$≈1.7)
如图,小明在A处用测角仪观测一座山的山顶B的仰角为45°,然后他前进了50米到达D处,观测B处的仰角为60°,求小山的高度BC(结果要求精确到1米,参考数据:$\sqrt{3}$≈1.7) 分析 根据等腰直角三角形的性质得到AC=BC,在Rt△BCD中,根据三角函数的定义得到CD=$\frac{BC}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$BC,通过AD=AC-CD=BC-$\frac{\sqrt{3}}{3}$BC=50,解得BC≈39米.
解答 解:∵BC⊥AC,∠BAC=45°,
∴AC=BC,
在Rt△BCD中,tan∠BDC=$\frac{BC}{CD}$,
即tan60°=$\frac{BC}{CD}$=$\sqrt{3}$,
∴CD=$\frac{BC}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$BC,
∴AD=AC-CD=BC-$\frac{\sqrt{3}}{3}$BC=50,
解得:BC≈39.
答:小山的高度BC约为39米.
点评 本题考查的是解直角三角形的应用-仰角俯角问题,掌握仰角和俯角的概念、正确运用锐角三角函数的概念是解题的关键.


 培优口算题卡系列答案
培优口算题卡系列答案 开心口算题卡系列答案
开心口算题卡系列答案 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d-2a=10,则数轴上原点应是( )
数轴上点A,B,C,D对应的有理数都是整数,若点A对应有理数a,点D对应有理数d,且d-2a=10,则数轴上原点应是( )| A. | A点 | B. | B点 | C. | C点 | D. | D点 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com