
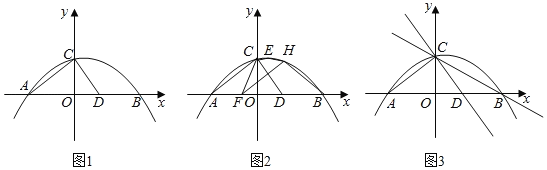
【题目】如图1,二次函数y![]() x2
x2![]() x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.
x+3的图象交x轴于A、B两点(点A在点B的左侧),交y轴于C点,连结AC,过点C作CD⊥AC交AB于点D.
(1)求点D的坐标;
(2)如图2,已知点E是该二次函数图象的顶点,在线段AO上取一点F,过点F作FH⊥CD,交该二次函数的图象于点H(点H在点E的右侧),当五边形FCEHB的面积最大时,求点H的横坐标;
(3)如图3,在直线BC上取一点M(不与点B重合),在直线CD的右上方是否存在这样的点N,使得以C、M、N为顶点的三角形与△BCD全等?若存在,请求出点N的坐标;若不存在,请说明理由.
【答案】(1)D(![]() ,0);(2)H的横坐标为
,0);(2)H的横坐标为![]() ;(3)满足要标的N点坐标有:(
;(3)满足要标的N点坐标有:(![]() ,
,![]() )、(3
)、(3![]() ,3)、(
,3)、(![]() ,
,![]() ).
).
【解析】
(1)先根据抛物线解析式求出A、B、C的坐标,由射影定理可得OD长度,从而求出D点坐标;
(2)设H点的横坐标为m,然后将五边形FCEHB的面积表示成关于m的二次函数,利用配方法可求得面积的最大值以及对应的H点坐标;
(3)由B、C、D的坐标可以求得DC、DB、BC的长度,然后分类讨论,分别画出符合要求的对应图形进行计算即可.
(1)令x=0,则y=3,∴C(0,3),∴OC=3.
令y=0,则![]() x2
x2![]() x+3=0,
x+3=0,
解得:x1=﹣4,x2=6,
∴A(﹣4,0),B(6,0),∴OA=4,OB=6.
∵CD⊥AC,∴∠ACD=90°.
![]()
∵CO⊥AD,
![]()
![]()
![]()
![]()
∴OC2=OAOD,
∴OD![]() ,∴D(
,∴D(![]() ,0).
,0).
(2)∵y![]() x2
x2![]() x+3
x+3![]() (x﹣1)2
(x﹣1)2![]() ,
,
∴E(1,![]() ).
).
如图2,连接OE、BE,作HG⊥x轴于点G,交BE于点P.

由B、E两点坐标可求得直线BE的解析式为:y![]() x
x![]() .
.
设H(m,![]() m2
m2![]() m+3),则P(m,
m+3),则P(m,![]() m
m![]() ),
),
∴HG![]() m2
m2![]() m+3,HP=
m+3,HP=![]()
![]() m2
m2![]() m
m![]() ,
,
∴S△BHE![]() (xB﹣xE)HP
(xB﹣xE)HP![]() (
(![]() m2
m2![]() m
m![]() )
)![]() m2
m2![]() m
m![]() .
.

∵FH⊥CD,AC⊥CD,∴AC∥FH,∴∠HFG=∠CAO.
∵∠AOC=∠FGH=90°,∴△ACO△FHG,
∴![]() ,∴FG
,∴FG![]() HG
HG![]() m2
m2![]() m+4,
m+4,
∴AF=AG﹣FG=m+4![]() m2
m2![]() m﹣4
m﹣4![]() m2
m2![]() m,
m,
∴S△AFC![]() AFOC
AFOC![]() (
(![]() m2
m2![]() m)
m)![]() m2+m.
m2+m.
∵S四边形ACEB=S△ACO+S△OCE+S△OEB![]() 4×3
4×3![]() 3×1
3×1![]() 6
6![]() ,
,
∴S五边形FCEHB=S四边形ACEB+S△BHE﹣S△AFC![]() (
(![]() m2
m2![]() m
m![]() )﹣(
)﹣(![]() m2+m
m2+m
![]() m2
m2![]() m+15
m+15![]() (m
(m![]() )2
)2![]() ,
,
∴当m![]() 时,S五边形FCEHB取得最大值
时,S五边形FCEHB取得最大值![]() .
.
此时,H的横坐标为![]() .
.
(3)∵B(6,0),C(0,3),D(![]() ,0),
,0),
∴CD=BD![]() ,BC=3
,BC=3![]() ,
,
∴∠DCB=∠DBC.
①如图3﹣1,△CMN≌△DCB,MN交y轴于K,

则CM=CN=DC=DB![]() ,MN=BC=3
,MN=BC=3![]() ,∠CMN=∠CNM=∠DBC=∠DCB,∴MN∥AB,∴MN⊥y轴,
,∠CMN=∠CNM=∠DBC=∠DCB,∴MN∥AB,∴MN⊥y轴,
∴∠CKN=∠COB=90°,MK=NK![]() MN
MN![]() ,
,
∴△CKN△COB,∴![]() ,
,
∴CK![]() ,∴OK=OC+CK
,∴OK=OC+CK![]() ,
,
∴N(![]() ,
,![]() ).
).
②如图3﹣2

则CN=CB=3![]() ,∠MCN=∠DBC,
,∠MCN=∠DBC,
∴CN∥AB,∴N(3![]() ,3).
,3).
③如图3﹣3,△CMN≌△DBC,

则∠CMN=∠DCB,CM=CN=DC=DB![]() ,MN=BC=3
,MN=BC=3![]() ,
,
∴MN∥CD,
作MR⊥y轴于R,
则![]() ,
,
∴CR![]() ,RM
,RM![]() ,
,
∴OR=3![]() ,
,
作MQ∥y轴,NQ⊥MQ于点Q,
则∠NMQ=∠DCO,∠NQM=∠DOC=90°,
∴△COD△MQN,∴![]() ,
,
∴MQ![]() MN
MN![]() ,NQ
,NQ![]() MN
MN![]() ,
,
∴NQ﹣RM![]() ,OR+MQ
,OR+MQ![]() ,
,
∴N(![]() ,
,![]() ).
).
综上所述:满足要标的N点坐标有:
(![]() ,
,![]() )、(3
)、(3![]() ,3)、(
,3)、(![]() ,
,![]() ).
).


科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 内接于直径为
内接于直径为![]() 的圆,
的圆,![]() .
.
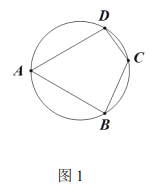
(1)①![]() _ ;
_ ;
②四边形![]() 的周长最大值为_ ;
的周长最大值为_ ;
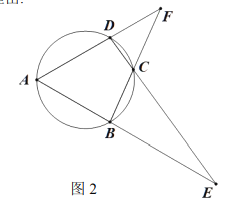
![]() 如图2,延长
如图2,延长![]() 相交于点
相交于点![]() ,延长
,延长![]() 相交于点
相交于点![]() 求
求![]() 与的
与的![]() 积;
积;
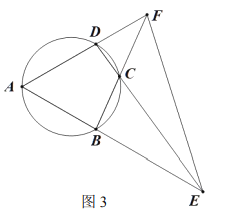
![]() 如图3,连接
如图3,连接![]() 请问在线段
请问在线段![]() 上是否存在点
上是否存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,若存在,请证明;若不存在,请说明理由.
对称,若存在,请证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的两个内角α,β满足α+2β=90°,那么我们称这样的三角形为“非常三角形”.
(1)若△ABC是“非常三角形”,∠C>90°,∠A=50°,则∠B= .
(2)如图,△ABC中,AB=AC,D是边BC上一点,以BD为直径的⊙O经过点A,连结AD.

①求证:△ADC为“非常三角形”.
②若sinB=![]() ,AB=8,弦AB上是否存在一点P,使得△BDP是“非常三角形”,若存在,请求出线段AP的长度;若不存在,请说明理由.
,AB=8,弦AB上是否存在一点P,使得△BDP是“非常三角形”,若存在,请求出线段AP的长度;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
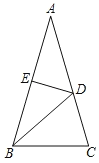
【题目】如图,在△ABC中,AB=AC,∠A=36°,BD平分∠ABC交AC于点D,点E是AB的中点,连结DE.
(1)求证:△ABD是等腰三角形;
(2)求∠BDE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为落实“停课不停学”,某校在线上教学时,要求学生因地制宜开展体育锻炼.为了解学生居家体育锻炼情况,学校对学生四月份平均每天开展体育锻炼的时长情况随机抽取了部分同学进行问卷调查,将调查结果进行了统计分析,并绘制如下两幅不完整的统计图:
(![]() 类:时长
类:时长![]() 分钟;
分钟;![]() 类:
类:![]() 分钟<时长
分钟<时长![]() 分钟;
分钟;![]() 类:
类:![]() 分钟<时长
分钟<时长![]() 分钟;
分钟;![]() 类:
类:![]() 分钟<时长
分钟<时长![]() 分钟;
分钟;![]() 类:时长
类:时长![]() 分钟).
分钟).
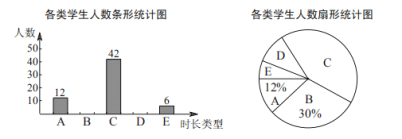
该校共有学生![]() 人,请根据以上统计分析,估计该校四月份平均每天体育锻炼时长超过
人,请根据以上统计分析,估计该校四月份平均每天体育锻炼时长超过![]() 分钟且不超过
分钟且不超过![]() 分钟的学生约有________人.
分钟的学生约有________人.
查看答案和解析>>
科目:初中数学 来源: 题型:
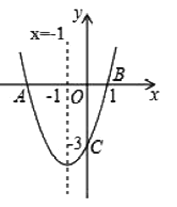
【题目】如图,二次函数的图象![]() 与
与![]() 轴交于点
轴交于点![]() 两点;与
两点;与![]() 轴交于点
轴交于点![]() ;对称轴为直线
;对称轴为直线![]() ,点
,点![]() 的坐标为
的坐标为![]() ,则下列结论:①
,则下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ,⑤
,⑤![]() 其中正确的结论个数是( )
其中正确的结论个数是( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】水果店张阿姨以每千克2元的价格购进柑桔若干千克,以每千克4元的价格出售,每天可售出50千克,通过调查发现,这种柑桔每千克的售价每降低0.1元,每天可多售出10千克,为保证每天至少售出130千克,张阿姨决定降价销售.
(1)若将柑桔每千克的售价降低x元,则每天的销售量是________千克(用含x的代数式表示);
(2)要想销售柑桔每天盈利150元,张阿姨需将每千克的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
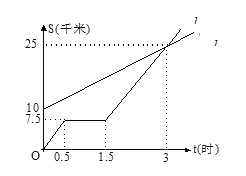
【题目】如图![]() 分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距 千米;
(2)走了一段路后,自行车发生故障,B进行修理,所用的时间是 小时;
(3)B第二次出发后 小时与A相遇;
(4)若B的自行车不发生故障,保持出发时的速度前进,则出发多长时间与A相遇?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com