
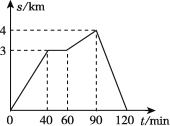
【题目】某人沿一条直路行走,此人离出发地的距离s(km)与行走时间t(min)的关系如图所示,请根据图中提供的信息回答下列问题:
(1)此人在这次行走过程中,停留的时间为 ;
(2)求此人在0~40min这段时间内行走的速度是多少千米/时;
(3)此人在这次行走过程中共走了多少千米?
 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】新定义:对非负数“四舍五入”到个位的值记为![]() ,即当
,即当![]() 为非负整数时,若
为非负整数时,若![]() ,则
,则![]() 如:
如:![]() ,试解决下列问题
,试解决下列问题
(1)填空:①![]() ②若
②若![]() ,则实数
,则实数![]() 的取值范围为
的取值范围为
(2)在关于![]() 的方程组
的方程组![]() 中,若未知数
中,若未知数![]() 满足
满足![]() ,求
,求![]() 的值.
的值.
(3)当![]() 时,若
时,若![]() ,求
,求![]() 的最小值.
的最小值.
(4)求满足![]() 的所有非负实数
的所有非负实数![]() 的值,请直接写出答案 .
的值,请直接写出答案 .
查看答案和解析>>
科目:初中数学 来源: 题型:
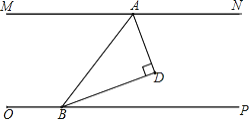
【题目】如图,![]() ,点
,点![]() 为直线
为直线![]() 上一定点,
上一定点,![]() 为直线
为直线![]() 上的动点,在直线
上的动点,在直线![]() 与
与![]() 之间且在线段
之间且在线段![]() 的右方作点
的右方作点![]() ,使得
,使得![]() .设
.设![]() 为锐角).
为锐角).
(1)求![]() 与
与![]() 的和;(提示过点
的和;(提示过点![]() 作
作![]()
(2)当点![]() 在直线
在直线![]() 上运动时,试说明
上运动时,试说明![]() ;
;
(3)当点![]() 在直线
在直线![]() 上运动的过程中,若
上运动的过程中,若![]() 平分
平分![]() ,
,![]() 也恰好平分
也恰好平分![]() ,请求出此时
,请求出此时![]() 的值
的值
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙在一段长2000米的直线公路上进行跑步练习,起跑时甲在起点,乙在甲的前面,若甲、乙同时起跑至甲到达终点的过程中,甲乙之间的距离y(米)与 时间x(秒)之间的函数关系如图所示.有下列说法:
①甲的速度为5米/秒;②100秒时甲追上乙;③经过50秒时甲乙相距50米;④甲到终点时,乙距离终点300米.其中正确的说法有( )

A. 4个 B. 3个
C. 2个 D. 1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中∠ADC=∠ABC=90°,AD=CD,DP⊥AB于点P,若四边形ABCD的面积是9,则DP的长是________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形组成的正方形网格中,建立如图所示的平面直角坐标系,已知△ABC的三个顶点都在格点上。
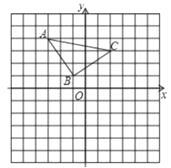
(1)请作出△ABC关于x轴对称的△A′B′C′,并分别写出点A′,B′,C′的坐标。
(2)在格点上是否存在一点D,使A,B,C,D四点为顶点的四边形是平行四边形,若存在,直接写出D点的坐标(只需写出一点即可)。
查看答案和解析>>
科目:初中数学 来源: 题型:
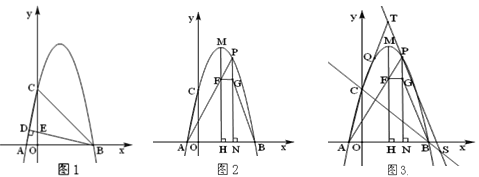
【题目】如图,抛物线y=-(x+k)(x-5)交x轴于点A、B(A左B右),交y轴交于点C,BD⊥AC垂足为D,BD与OC交于点E,且CE=4OE.
⑴如图1,求抛物线的解析式;
⑵如图2,点M为抛物线的顶点,MH⊥x轴,垂足为H,点P为第一象限MH右侧抛物线上一点,PN⊥x轴于点N,PA交MH于点F,FG⊥PN于点G,求tan∠GBN的值;
⑶如图3,在⑵的条件下,过点P作BG的平行线交直线BC于点S,点T为直线PS上一点,TC交抛物线于点Q,若CQ=QT,TS=![]() ,求点P的坐标.
,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图△ABC中,∠A=96°,延长BC到D,∠ABC与∠ACD的平分线相交于点A1∠A1BC与∠A1CD的平分线相交于点A2,依此类推,∠A4BC与∠A4CD的平分线相交于点A5,则∠A5的度数为( )

A. 19.2° B. 8° C. 6° D. 3°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先阅读理解下面的例题,再按要求解答下列问题:
例题:对于![]() ,这类不等式我们可以进行下面的解题思路 由有理数的乘法法则两数相乘,同号得正,可得;
,这类不等式我们可以进行下面的解题思路 由有理数的乘法法则两数相乘,同号得正,可得;
![]() 或
或![]() , 从而将陌生的高次不等式化为了学过的一元一次不等式组,分别去解两个不等式组即可求得原不等式组的解集,即: 解不等式组(1)得
, 从而将陌生的高次不等式化为了学过的一元一次不等式组,分别去解两个不等式组即可求得原不等式组的解集,即: 解不等式组(1)得![]() ,解不等式组(2)得
,解不等式组(2)得![]() ,所以
,所以![]() 的解集为
的解集为![]() 或
或![]() .请利用上述解题思想解决下面的问题:
.请利用上述解题思想解决下面的问题:
(1)请直接写出![]() 的解集.
的解集.
(2)对于![]() ,请根据有理数的除法法则化为我们学过的不等式(组).
,请根据有理数的除法法则化为我们学过的不等式(组).
(3)求不等式![]() 的解集.
的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com