
【题目】如图,抛物线y=-(x+k)(x-5)交x轴于点A、B(A左B右),交y轴交于点C,BD⊥AC垂足为D,BD与OC交于点E,且CE=4OE.
⑴如图1,求抛物线的解析式;
⑵如图2,点M为抛物线的顶点,MH⊥x轴,垂足为H,点P为第一象限MH右侧抛物线上一点,PN⊥x轴于点N,PA交MH于点F,FG⊥PN于点G,求tan∠GBN的值;
⑶如图3,在⑵的条件下,过点P作BG的平行线交直线BC于点S,点T为直线PS上一点,TC交抛物线于点Q,若CQ=QT,TS=![]() ,求点P的坐标.
,求点P的坐标.
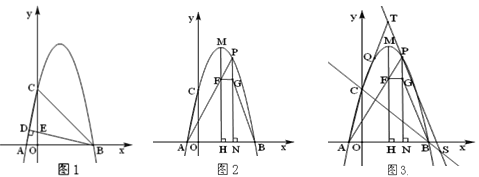
【答案】(1)y=-x2+4x+5;(2)3;(3)P1(3,8),P2(4,5)
【解析】
(1)通过证明△OCA≌△OBE得OC=OB,从而求出k的值,故可得解.
(2) 由y=-x2+4x+5=-(x-2)2+9知对称轴x=2,AH=3. 设P(m,-m2+4m+5),得tan∠PAN=![]() =
=![]() ,由FH=3(5-m)=GN,BN=5-m得tan∠GBN=3;
,由FH=3(5-m)=GN,BN=5-m得tan∠GBN=3;
(3)设Q(t,-t2+4t+5),T(x,y),由QC=QT得T(2t,-2t2+8t-5);过点T、S分别作x轴、y轴的平行线,相较于点K,易求TK=4,KS=12,得S(2t+4,-2t2+8t-7),设直线BC解析式为y=k1x+b,得y=-x+5,作SL⊥PN,tan∠PSL=tan∠1=3,设P(m,-m2+4m+5)则PL=3LS,求得m1=3,m2=4,得P1(3,8),P2(4,5).
(1)令y=0,则x=5,x=-k
∴A(-k,0),B(5,0),C(0,5k);
∴OC=5k,OA=k,
∵OC=5OE,
∴OE=k=OA,
∴△OCA≌△OBE,
∴OC=OB,
∴5k=5,
∴k=1,
∴抛物线为:y=-x2+4x+5;
(2)y=-x2+4x+5=(x+2)2+1
∴对称轴x=2,AH=3,;
设P(m,-m2+4m+5)
tan∠PAN=![]() =
=![]() =5-m=
=5-m=![]()
∴FH=3(5-m)=GN,BN=5-m.;
∴tan∠GBN=![]() =3;
=3;
(3)设Q(t,-t2+4t+5),C(0,5),
∵QC=QT,
∴Qx-Cx=Tx-Qx,Qy-Cy=Ty-Qy
设T(x,y)
∴t-0=x-t
-t2+4t+5-5=y- (-t2+4t+5)
∴x=2t,y=-2t2+8t-5,∴T(2t,-2t2+8t-5);
过点T、S分别作x轴、y轴的平行线,相较于点K
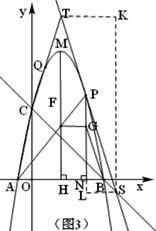
∴∠TKS=90°
∵PS∥BG
∴∠GBN=∠1=∠KTS,∴tan∠KTS=3
∵TS=4![]() ,∴TK=4,KS=12
,∴TK=4,KS=12
∴S(2t+4,-2t2+8t-7);
设直线BC解析式为:y=k1x+b,B(5,0),C(0,5)
∴y=-x+5;
∵-2t2+8t-7=2t-4+5,t2-5t+4=0,t1=1,t2=4(舍),
∴S(6,-1);
作SL⊥PN,tan∠PSL=tan∠1=3
设P(m,-m2+4m+5)则PL=-m2+4m+5+1=-m2+4m+6,SL=6-m
∴PL=3LS,
∴-m2+4m+6=18-3m,m2-7m+12=0,
∴m1=3,m2=4
∴P1(3,8),P2(4,5)


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】为发展学生的核心素养,培养学生的综合能力,某学校计划开设四门选修课:乐器、舞蹈、绘画、书法.学校采取随机抽样的方法进行问卷调查(每个被调查的学生必须选择而且只能选择其中一门).对调查结果进行整理,绘制成如下两幅不完整的统计图,请结合图中所给信息解答下列问题:
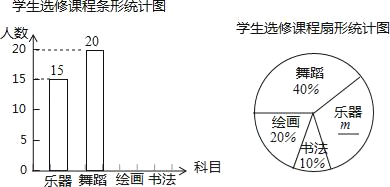
(1)本次调查的学生共有 人,在扇形统计图中,m的值是 ;
(2)将条形统计图补充完整;
(3)在被调查的学生中,选修书法的有2名女同学,其余为男同学,现要从中随机抽取2名同学代表学校参加某社区组织的书法活动,请写出所抽取的2名同学恰好是1名男同学和1名女同学的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,A,B两点在数轴上,A点对应的有理数是﹣2,线段AB=12,点P从点A出发,沿AB以每秒1个单位长度的速度向终点B匀速运动;同时点Q从点B出发,沿BA以每秒2个单位长度的速度向终点A匀速运动,设运动时间为ts
(1)请在数轴上标出原点O和B点所对应的有理数:
(2)直接写出PA= ,BQ= (用含t的代数式表示);
(3)当P,Q两点相遇时,求t的值;
(4)当P,Q两点相距5个单位长度时,直接写出线段PQ的中点对应的有理数.
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
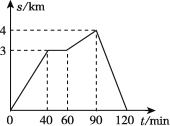
【题目】某人沿一条直路行走,此人离出发地的距离s(km)与行走时间t(min)的关系如图所示,请根据图中提供的信息回答下列问题:
(1)此人在这次行走过程中,停留的时间为 ;
(2)求此人在0~40min这段时间内行走的速度是多少千米/时;
(3)此人在这次行走过程中共走了多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
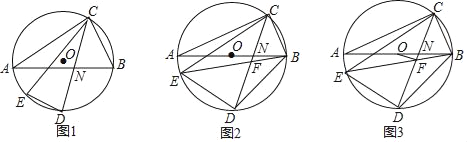
【题目】如图,△ABC内接于⊙O,弦CD平分∠ACB,点E为弧AD上一点,连接CE、DE,CD与AB交于点N.
(1)如图1,求证:∠AND=∠CED;
(2)如图2,AB为⊙O直径,连接BE、BD,BE与CD交于点F,若2∠BDC=90°﹣∠DBE,求证:CD=CE;
(3)如图3,在(2)的条件下,连接OF,若BE=BD+4,BC=![]() ,求线段OF的长.
,求线段OF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形BCDE的各边分别平行于x轴与y轴,物体甲和物体乙由点A(2,0)同时出发,沿矩形BCDE的边作环绕运动,物体甲按逆时针方向以1个单位/秒匀速运动,物体乙按顺时针方向以2个单位/秒匀速运动,则两个物体运动后的第2018次相遇地点的坐标是( )

A. (1,﹣1) B. (2,0) C. (﹣1,1) D. (﹣1,﹣1)
查看答案和解析>>
科目:初中数学 来源: 题型:
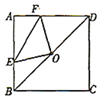
【题目】如图,正方形![]() 的边长为4,点
的边长为4,点![]() 是对角线
是对角线![]() 的中点,点
的中点,点![]() 、
、![]() 分别在
分别在![]() 、
、![]() 边上运动,且保持
边上运动,且保持![]() ,连接
,连接![]() ,
,![]() ,
,![]() .在此运动过程中,下列结论:①
.在此运动过程中,下列结论:①![]() ;②
;②![]() ;③四边形
;③四边形![]() 的面积保持不变;④当
的面积保持不变;④当![]() 时,
时,![]() ,其中正确的结论是( )
,其中正确的结论是( )
A.①②B.②③C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,点![]() ,
,![]() ,
,![]() 都是格点.
都是格点.
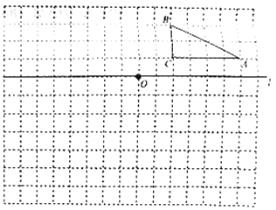
(1)将![]() 向左平移6个单位长度得到
向左平移6个单位长度得到![]() ,请画出
,请画出![]() ;
;
(2)将![]() 绕点
绕点![]() 按逆时针方向旋转
按逆时针方向旋转![]() 得到
得到![]() ,请画出
,请画出![]() ;
;
(3)作出![]() 关于直线
关于直线![]() 对称的
对称的![]() ,使
,使![]() ,
,![]() ,
,![]() 的对称点分别是
的对称点分别是![]() ,
,![]() ,
,![]() ;
;
(4)![]() 与
与![]() 成______,
成______,![]() 与
与![]() 成______(填“中心对称”或“轴对称”).如果成中心对称请你在图中确定其对称中心点
成______(填“中心对称”或“轴对称”).如果成中心对称请你在图中确定其对称中心点![]() 的位置.
的位置.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com