
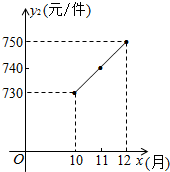
 某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:
某企业为重庆计算机产业基地提供电脑配件.受美元走低的影响,从去年1至9月,该配件的原材料价格一路攀升,每件配件的原材料价格y1(元)与月份x(1≤x≤9,且x取整数)之间的函数关系如下表:| 月份x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
| 价格y1(元/件) | 560 | 580 | 600 | 620 | 640 | 660 | 680 | 700 | 720 |
分析 (1)把表格(1)中任意2点的坐标代入直线解析式可得y1的解析式.把(10,730)(12,750)代入直线解析式可得y2的解析式,
(2)分情况探讨得:1≤x≤9时,利润=P1×(售价-各种成本);10≤x≤12时,利润=P2×(售价-各种成本);并求得相应的最大利润即可;
(3)根据1至5月的总利润1700万元得到关系式求值即可.
解答 解:(1)设y1=kx+b,则$\left\{\begin{array}{l}{k+b=560}\\{2k+b=580}\end{array}\right.$,
解得$\left\{\begin{array}{l}{k=20}\\{b=540}\end{array}\right.$.
∴y1=20x+540(1≤x≤9,且x取整数);
设y2=ax+b,则$\left\{\begin{array}{l}{10a+b=730}\\{12a+b=750}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=10}\\{b=630}\end{array}\right.$.
∴y2=10x+630(10≤x≤12,且x取整数);
(2)设去年第x月的利润为W万元.
1≤x≤9,且x取整数时,W=P1×(1000-50-30-y1)=-2x2+16x+418=-2(x-4)2+450,
∴x=4时,W最大=450万元;
10≤x≤12,且x取整数时,W=P2×(1000-50-30-y2)=(x-29)2,
∴x=10时,W最大=361万元;
∵450万元>361万元,
∴4月份利润最大,最大利润是450万元;
(3)去年12月的销售量为-0.1×12+2.9=1.7(万件),
今年原材料价格为:750+60=810(元)
今年人力成本为:50×(1+20%)=60元.
∴5×[1000×(1+a%)-810-60-30]×1.7(1-0.1×a%)=1700,
设t=a%,整理得10t2-99t+10=0,
解得t=$\frac{99±\sqrt{9401}}{20}$,
∵9401更接近于9409,
∴$\sqrt{9401}$≈97,
∴t1≈0.1,t2≈9.8,
∴a1≈10或a2≈980,
∵1.7(1-0.1×a%)≥1,
∴a≈10.
答:a的整数解为10.
点评 本题综合考查了一次函数和二次函数的应用;根据二次函数的最值及相应的取值范围得到一定范围内的最大值是解决本题的易错点;利用估算求得相应的整数解是解决本题的难点.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:解答题
 如图,△ABC内接于⊙O,AB是直径,D是$\widehat{AC}$上的点,BD交AC于点E,过点B作⊙O的切线与AC的延长线交于点F,已知AB=5,sin∠CAB=$\frac{3}{5}$,求CF的长.
如图,△ABC内接于⊙O,AB是直径,D是$\widehat{AC}$上的点,BD交AC于点E,过点B作⊙O的切线与AC的延长线交于点F,已知AB=5,sin∠CAB=$\frac{3}{5}$,求CF的长.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
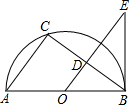 如图,AB是半圆O直径,点C是⊙O上一点,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,使∠OEB=∠ABC.
如图,AB是半圆O直径,点C是⊙O上一点,过点O作OD∥AC交BC于点D,在OD的延长线上取一点E,使∠OEB=∠ABC.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com