
【题目】如图,点C在线段BD上,AC⊥BD,CA=CD,点E在线段CA上,且满足DE=AB,连接DE并延长交AB于点F. 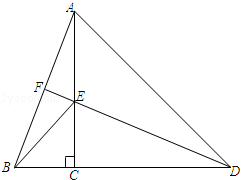
(1)求证:DE⊥AB;
(2)若已知BC=a,AC=b,AB=c,设EF=x,则△ABD的面积用代数式可表示为;S△ABD= ![]() c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
c(c+x)你能借助本题提供的图形,证明勾股定理吗?试一试吧.
【答案】
(1)证明:在Rt△ABC和Rt△DCE中,
![]()
∴Rt△ABC≌Rt△DCE(HL)
∴∠BAC=∠EDC(全等三角形的对应角相等),
∵∠AEF=∠DEC(对顶角相等),∠EDC+∠DEC=90°(直角三角形两锐角互余),
∴∠BAC+∠AEF=∠EDC+∠DEC=90°.
∴∠AFE=180°﹣(∠BAC+∠AEF)=90°.
∴DE⊥AB
(2)解:由题意知:
S△ABD=S△BCE+S△ACD+S△ABE= ![]() a2+
a2+ ![]() b2+
b2+ ![]() cx,
cx,
∵ ![]() ,
,
∴ ![]() .
.
∴a2+b2=c2
【解析】(1)首先证明Rt△ABC≌Rt△DCE,得出∠BAC=∠EDC,进而求出∠AFE=180°﹣(∠BAC+∠AEF)=90°,即可得出答案;(2)根据S△ABD=S△BCE+S△ACD+S△ABE , ![]() 得出a2+b2=c2即可.
得出a2+b2=c2即可.


科目:初中数学 来源: 题型:
【题目】探究规律:如图,已知直线m∥n,A、B为直线n上的两点,C、P为直线m上的两点. 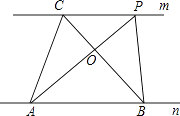
(1)请写出图中面积相等的各对三角形: .
(2)如果A、B、C为三个定点,点P在m上移动,那么无论P点移动到任何位置总有:与△ABC的面积相等;理由是: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】观察下列算式:1×5+4=32 , 2×6+4=42 , 3×7+4=52 , 4×8+4=62 , 请你在观察规律之后并用你得到的规律填空:× +=502 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,∠ABD和∠BDC的平分线交于E , BE交CD于点F , ∠1+∠2=90°.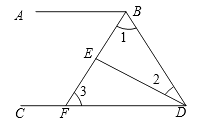
(1)试说明:AB∥CD;
(2)若∠2=25°,求∠BFC的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王计划用100元钱买乒乓球,所购买球的个数为W个,每个球的单价为n元,其中( )
A. 100是常量,W,n是变量 B. 100,W是常量,n是变量
C. 100,n是常量,W是变量 D. 无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由实验测得某一弹簧的长度y(cm)与悬挂物体的质量x(kg)之间有如下关系:y= —12+0.5x.下列说法正确的是( )
A. 变量是x,常量是12,0.5 B. 变量是x,常量是-12,0.5
C. 变量是x,y,常量是12,0.5 D. 变量是x,y,常量是-12,0.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知射线AB与直线CD交于点O,OF平分∠BOC,OG⊥OF于O,AE∥OF,且∠A=30°. 
(1)求∠DOF的度数;
(2)试说明OD平分∠AOG.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com