
【题目】如图,在平面直角坐标系中,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交与A(4,-2),B(-2,n)两点,与
的图像交与A(4,-2),B(-2,n)两点,与![]() 轴交与点C.
轴交与点C.
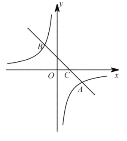
(1)求![]() ,n的值;
,n的值;
(2)请直接写出不等式![]() 的解集;
的解集;
(3)点A关于![]() 轴对称得到点A’,连接A’B,A’C,求△A’BC的面积.
轴对称得到点A’,连接A’B,A’C,求△A’BC的面积.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]() ;(3)8.
;(3)8.
【解析】
(1)将A点坐标代入![]() 即可求得
即可求得![]() 的值,再根据求得的解析式即可求得n的值;
的值,再根据求得的解析式即可求得n的值;
(2)用函数的观察,反比例函数图象在一次函数图象上面部分的x取值范围,即为不等式的解集;
(3)求出对称点坐标,再根据![]() 即可求得面积.
即可求得面积.
解:(1)将A(4,-2)代入![]() ,得k2=-8,
,得k2=-8,
∴![]() ,
,
将(-2,n)代入![]() 得n=4,
得n=4,
∴k2=-8,n=4;
(2)根据函数图象可知![]() 的解集为:-2<x<0或x>4;
的解集为:-2<x<0或x>4;
(3)将A(4,-2),B(-2,4)代入y=k1x+b,得k1=-1,b=2
∴一次函数的关系式为y=-x+2,
与x轴交于点C(2,0),
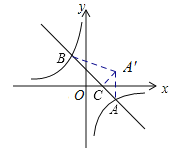
∴图象沿x轴翻折后,得A′(4,2),
![]() .
.
∴△A'BC的面积为8.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的顶点坐标为
的顶点坐标为![]() ,且与
,且与![]() 轴交于点C
轴交于点C![]() ,与
,与![]() 轴交于A、B两点(点A在点B的右侧).
轴交于A、B两点(点A在点B的右侧).
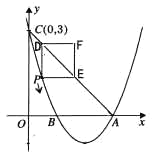
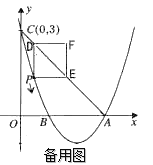
(1)求该抛物线的函数关系式;
(2)点P是该抛物线上一动点,从点C沿抛物线向点A运动(点P与A不重合),过点P作PD∥![]() 轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
轴,交直线AC于点D;作PE∥x轴,交直线AC于点E,以PD,PE为边的矩形PEFD,问矩形PEFD周长是否存在最大值?若存在,求出此时P点的坐标及最大值;若不存在,请说明理由;
(3)在问题(2)的条件下,P点满足∠DAP=90°,且点E在![]() 轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
轴上,点F在抛物线上,问是否存在以A、P、E、F为顶点的平行四边形?若存在,求点F的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
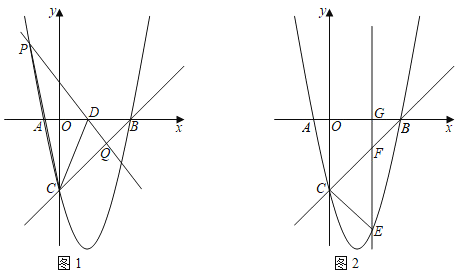
【题目】抛物线y=ax2+bx﹣5的图象与x轴交于A、B两点,与y轴交于点C,其中点A坐标为(﹣1,0),一次函数y=x+k的图象经过点B、C.
(1)试求二次函数及一次函数的解析式;
(2)如图1,点D(2,0)为x轴上一点,P为抛物线上的动点,过点P、D作直线PD交线段CB于点Q,连接PC、DC,若S△CPD=3S△CQD,求点P的坐标;
(3)如图2,点E为抛物线位于直线BC下方图象上的一个动点,过点E作直线EG⊥x轴于点G,交直线BC于点F,当EF+![]() CF的值最大时,求点E的坐标.
CF的值最大时,求点E的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果关于![]() 的一元二次方程
的一元二次方程![]() 有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.
有两个不相等的实数根,且其中一个根为另一个根的一半,则称这样的方程为“半等分根方程”.
(1)①方程![]() 半等分根方程(填“是”或“不是”);
半等分根方程(填“是”或“不是”);
②若![]() 是半等分根方程,则代数式
是半等分根方程,则代数式![]() ;
;
(2)若点![]() 在反比例函数
在反比例函数![]() 的图象上,则关于
的图象上,则关于![]() 的方程
的方程![]() 是半等分根方程吗?并说明理由;
是半等分根方程吗?并说明理由;
(3)如果方程![]() 是半等分根方程,且相异两点
是半等分根方程,且相异两点![]() ,
,![]() 都在抛物线
都在抛物线![]() 上,试说明方程
上,试说明方程![]() 的一个根为
的一个根为![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某社区今年准备新建一养老中心,其中规划建造三类养老专用房间共100间,这三类养老专用房间分别为单人间(1个养老床位),双人间(2个养老床位),三人间(3个养老床位),因实际需要,单人间房间数在10至30之间(包括10和30),且双人间的房间数是单人间的2倍,设规划建造单人间的房间数为![]() .
.
(1)根据题意,填写下表:
单人间的房间数 | 10 | … |
| … | 30 |
双人间的房间数 | _________ | … |
| … | 60 |
三人间的房间数 | 70 | … | _________ | … | _________ |
养老床位数 | 260 | … | _________ | … | _________ |
(2)若该养老中心建成后可提供养老床位200个,求![]() 的值;
的值;
(3)求该养老中心建成后最多提供养老床位多少个?最少提供养老床位多少个?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两个草莓采摘园为吸引顾客,在草莓销售价格相同的基础上分别推出优惠方案,甲园:顾客进园需购买门票,采摘的草莓按六折优惠.乙园:顾客进园免门票,采摘草莓超过一定数量后,超过的部分打折销售.活动期间,某顾客的草莓采摘量为x kg,若在甲园采摘需总费用y1元,若在乙园采摘需总费用y2元, y1,y2与x之间的函数图象如图所示,则下列说法中错误的是( )
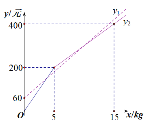
A.甲园的门票费用是60元
B.草莓优惠前的销售价格是40元/kg
C.乙园超过5 kg后,超过的部分价格优惠是打五折
D.若顾客采摘12 kg草莓,那么到甲园或乙园的总费用相同
查看答案和解析>>
科目:初中数学 来源: 题型:
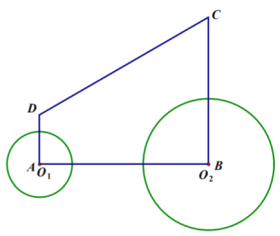
【题目】如图,直角梯形![]() 中,
中,![]() 的圆心
的圆心![]() 从点
从点![]() 开始沿折线
开始沿折线![]() 以
以![]() 的速度向点
的速度向点![]() 运动,
运动,![]() 的圆心
的圆心![]() 从点
从点![]() 开始沿
开始沿![]() 边以
边以![]()
![]() 的速度向点
的速度向点![]() 运动,
运动,![]() 半径为
半径为![]() 的半径为
的半径为![]() ,若
,若![]() 分别从点
分别从点![]() 、点
、点![]() 同时出发,运动的时间为
同时出发,运动的时间为![]()
(1)请求出![]() 与腰
与腰![]() 相切时
相切时![]() 的值;
的值;
(2)在![]() 范围内,当
范围内,当![]() 为何值时,
为何值时,![]() 与
与![]() 外切?
外切?
查看答案和解析>>
科目:初中数学 来源: 题型:
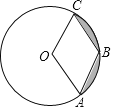
【题目】如图,已知⊙O的半径是2,点A、B、C在⊙O上,若四边形OABC为菱形,则图中阴影部分面积为( )
A. ![]() π﹣2
π﹣2![]() B.
B. ![]() π﹣
π﹣![]() C.
C. ![]() π﹣2
π﹣2![]() D.
D. ![]() π﹣
π﹣![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com