
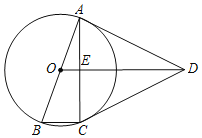
【题目】如图,四边形ABCD中,AB=AD=CD,以AB为直径的⊙O经过点C,连接AC、OD交于点E.
(1)求证:OD∥BC;
(2)若AC=2BC,求证:DA与⊙O相切.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)利用SSS可证明△OAD≌△OCD,可得∠ADO=∠CDO,根据等腰三角形“三线合一”的性质可得DE⊥AC,由AB是直径可得∠ACB=90°,即可证明OD//BC;
(2)设BC=a,则AC=2a,利用勾股定理可得AD=AB=![]() ,根据中位线的性质可用a表示出OE、AE的长,即可表示出OD的长,根据勾股定理逆定理可得∠OAD=90°,即可证明DA与⊙O相切.
,根据中位线的性质可用a表示出OE、AE的长,即可表示出OD的长,根据勾股定理逆定理可得∠OAD=90°,即可证明DA与⊙O相切.
(1)连接OC,
在△OAD和△OCD中,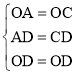 ,
,
∴△OAD≌△OCD(SSS),
∴∠ADO=∠CDO,
∵AD=CD,
∴DE⊥AC,
∵AB为⊙O的直径,
∴∠ACB=90°,
即BC⊥AC,
∴OD∥BC;
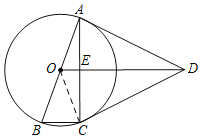
(2)设BC=a,
∵AC=2BC,
∴AC=2a,
∴AD=AB=![]() =
=![]() =
=![]() a,
a,
∵OE∥BC,且AO=BO,
∴OE为△ABC的中位线,
∴OE=![]() BC=
BC=![]() a,AE=CE=
a,AE=CE=![]() AC=a,
AC=a,
在△AED中,DE=![]() =
=![]() =2a,
=2a,
∴OD=OE+DE=![]() ,
,
在△AOD中,AO2+AD2=(![]() )2+(
)2+(![]() a)2=
a)2=![]() a2,OD2=(
a2,OD2=(![]() )2=
)2=![]() a2,
a2,
∴AO2+AD2=OD2,
∴∠OAD=90°,
∵AB是直径,
∴DA与⊙O相切.


科目:初中数学 来源: 题型:
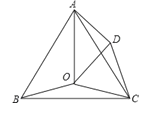
【题目】如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BOC绕点C按顺时针旋转得到△ADC,连接OD,OA.
(1)求∠ODC的度数;
(2)若OB=4,OC=5,求AO的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是二次函数![]() 的图象,下列结论:
的图象,下列结论:
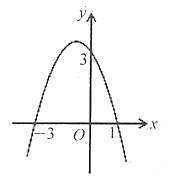
①二次三项式![]() 的最大值为
的最大值为![]() ;
;
![]() 使
使![]() 成立的
成立的![]() 的取值范围是
的取值范围是![]() ;
;
![]() 一元二次方程
一元二次方程![]() ,当
,当![]() 时,方程总有两个不相等的实数根;
时,方程总有两个不相等的实数根;
![]() 该抛物线的对称轴是直线
该抛物线的对称轴是直线![]() ;
;
![]()
其中正确的结论有______________ (把所有正确结论的序号都填在横线上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①、图②都是6×6的正方形网格,每个小正方形的边长均为1,每个小正方形的顶点叫做格点,线段AB的端点都在格点上,仅用无刻度的直尺,分别按下列要求画图,保留作图痕迹.
(1)在图①中画出一个以AB为一边的等腰△ABC,使点C在格点上,且面积为![]() ;
;
(2)在图②中画出一个以AB为一边的等腰△ABD,使点D在格点上,且tan∠DAB=3,并直接写出△ABD底边上的高.
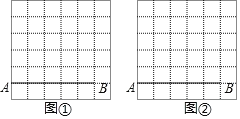
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2016年3月国际风筝节期间,王大伯决定销售一批风筝,经市场调研:蝙蝠型风筝进价每个为10元,当售价每个为12元时,销售量为180个,若售价每提高1元,销售量就会减少10个,请回答以下问题:
(1)用表达式表示蝙蝠型风筝销售量y(个)与售价x(元)之间的函数关系(12≤x≤30);
(2)王大伯为了让利给顾客,并同时获得840元利润,售价应定为多少?
(3)当售价定为多少时,王大伯获得利润W最大,最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本小题满分7分) 已知:如图,A是⊙O上一点,半径OC的延长线与过点A的直线交于B点,OC=BC,AC=![]() OB.
OB.
(1)求证:AB是⊙O的切线;
(2)若∠ACD=45°,OC=2,求弦CD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为某商场的一个可以自由转动的转盘,规定:顾客购物满100元即可获得一次转动转盘的机会,当转盘停止时,指针落在哪一个区域就获得相应的奖品.下表是活动进行中的一组统计数据:
转动转盘的次数 | 100 | 150 | 200 | 500 | 800 | 1000 |
落在“钦料”的次数m | 71 | 110 | 155 | 379 | 603 | 752 |
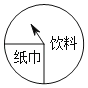
根据以上信息,解决下列问题:
(1)请估计转动该转盘一次,获得饮料的概率约是 (精确到0.01);
(2)现有若干个除颜色外相同的白球和黑球,根据(1)结论,在保证获得饮料与纸巾概率不变的情况下,请你设计一个可行的摸球抽奖规则,详细说明步骤;
(3)若小郑和小刘都购买超过100元的商品,均获得一次转动转盘的机会,请根据(2)中设计的规则,利用列表法或画树状图法求两人都获得“饮料”的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F,若BF=2,AF=3,则△ABC的面积是
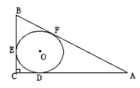
A.6B.7C.![]() D.12
D.12
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com