练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，在Rt△ABC中，∠ACB＝90°，⊙O是△ABC的内切圆，三个切点分别为D、E、F，若BF＝2，AF＝3，则△ABC的面积是

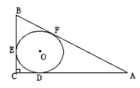
    A.6B.7C.D.12

    【答案】A

    【解析】

    利用切线的性质以及正方形的判定方法得出四边形OECD是正方形，进而利用勾股定理得出答案．

    连接DO，EO，

    ∵⊙O是△ABC的内切圆，切点分别为D，E，F，

    ∴OE⊥AC，OD⊥BC，CD=CE，BD=BF=3，AF=AE=4

    又∵∠C=90°，

    ∴四边形OECD是矩形，

    又∵EO=DO，

    ∴矩形OECD是正方形，

    设EO=x，

    则EC=CD=x，

    在Rt△ABC中

    BC2+AC2=AB2

    故（x+2）2+（x+3）2=52，

    解得：x=1，

    ∴BC=3，AC=4，

    ∴S△ABC=×3×4=6，

    故选A．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

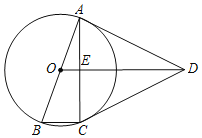
    【题目】如图，四边形ABCD中，AB＝AD＝CD，以AB为直径的⊙O经过点C，连接AC、OD交于点E．

    （1）求证：OD∥BC；

    （2）若AC＝2BC，求证：DA与⊙O相切．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

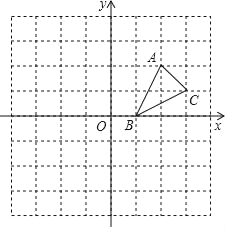
    【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）．

    （1）画出△ABC关于x轴对称的△A1B1C1；

    （2）画出将△ABC绕原点O按逆时针旋转90°所得的△A2B2C2，并写出点C2的坐标；

    （3）△A1B1C1与△A2B2C2成中心对称吗？若成中心对称，写出对称中心的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校为了解本校九年级学生足球训练情况，随机抽查该年级若干名学生进行测试，然后把测试结果分为4个等级：A、B、C、D，并将统计结果绘制成两幅不完整的统计图．请根据图中的信息解答下列问题：

    （1）在这次调查中，一共调查了 名学生，扇形统计图中，C等级对应的扇形圆心角是 　 　°.

    （2）补全条形统计图.

    （3）该年级共有900人，估计该年级足球测试成绩为D等的人数为　 　人.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】机械表是日常生活中常见的一类钟表，与电子表不同，机械表受环境、机芯等因素的影响常会产生走时误差．现为了比较市场上甲、乙两款机械表的精准度，从两款表中，各随机抽取一块进行每日走时误差的检测，连续检测10天，两款表每日走时误差的统计数据如图(单位：秒)：

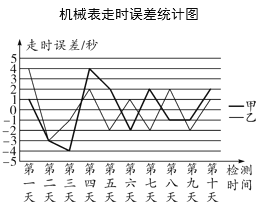
    （1）甲、乙两种机械表的平均走时误差分别是多少？

    （2）小明现计划购买一块机械表，如果仅从走时的准确度考虑，你会推荐他购买甲、乙哪一种，请说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在Rt△ABC中，CD为斜边AB上的高，AC=3，BC=4，分别用r、r1、r2、表示△ABC，△ACD，△BCD内切圆的半径，则(　　)

    A.r+r1+r2=B.r+r1+r2=

    C.r﹣r1﹣r2=﹣D.r﹣r1﹣r2=﹣

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图1，△ABC中，∠ACB=90°，CD⊥AB于D，E为BC中点，CF⊥AE于F．

    （1）求证：4CE2=BDAB；

    （2）若2∠DCF=∠ECF，求cos∠ECF的值；

    （3）如图2，DF延长线交BC于G，若AC=BC，EG=1，则DG=　 　．

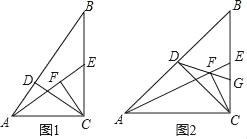
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】定义：

    我们知道，四边形的一条对角线把这个四边形分成了两个三角形，如果这两个三角形相似（不全等），我们就把这条对角线叫做这个四边形的“相似对角线”．

    理解：

    （1）如图1，已知Rt△ABC在正方形网格中，请你只用无刻度的直尺在网格中找到一点D，使四边形ABCD是以AC为“相似对角线”的四边形（保留画图痕迹，找出3个即可）；

    （2）如图2，在四边形ABCD中，∠ABC=80°，∠ADC=140°，对角线BD平分∠ABC．

    求证：BD是四边形ABCD的“相似对角线”；

    （3）如图3，已知FH是四边形EFCH的“相似对角线”，∠EFH=∠HFG=30°，连接EG，若△EFG的面积为2，求FH的长．

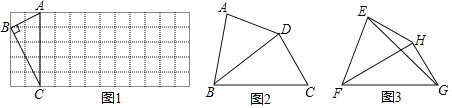
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，抛物线y=ax2+bx﹣经过点A（1，0）和点B（5，0），与y轴交于点C．

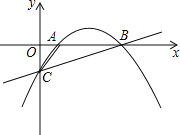
    （1）求此抛物线的解析式；

    （2）以点A为圆心，作与直线BC相切的⊙A，求⊙A的半径；

    （3）在直线BC上方的抛物线上任取一点P，连接PB，PC，请问：△PBC的面积是否存在最大值？若存在，求出这个最大值的此时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案