
【题目】在Rt△ABC中,CD为斜边AB上的高,AC=3,BC=4,分别用r、r1、r2、表示△ABC,△ACD,△BCD内切圆的半径,则( )
A.r+r1+r2=![]() B.r+r1+r2=
B.r+r1+r2=![]()
C.r﹣r1﹣r2=﹣![]() D.r﹣r1﹣r2=﹣
D.r﹣r1﹣r2=﹣![]()
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
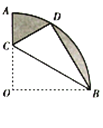
【题目】如图,在扇形OAB中,∠AOB=90°,半径OA=2.将扇形OAB沿过点B的直线折叠.点O恰好落在弧AB上点D处,折痕交OA于点C,则整个阴影部分的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】据天气预报报道,福建省部分城市某日的最高气温如下表所示:
城市 | 福州 | 厦门 | 宁德 | 莆田 | 泉州 | 漳州 | 龙岩 | 三明 | 南平 |
最高气温(℃) | 11 | 16 | 11 | 13 | 13 | 17 | 16 | 11 | 9 |
则下列说法正确的是( )
A.龙岩的该日最高气温最高B.这组数据的众数是16
C.这组数据的中位数是11D.这组数据的平均数是13
查看答案和解析>>
科目:初中数学 来源: 题型:
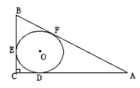
【题目】如图,在Rt△ABC中,∠ACB=90°,⊙O是△ABC的内切圆,三个切点分别为D、E、F,若BF=2,AF=3,则△ABC的面积是
A.6B.7C.![]() D.12
D.12
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两商场以同样价格出售同样的商品:并且又各自推出不同的优惠方案,在甲商场累计购物超过100元后,超出100元的部分按![]() 收费;在乙商场累计购物超过50元后,超出50元的部分按
收费;在乙商场累计购物超过50元后,超出50元的部分按![]() 收费.顾客到哪家商场购物花费少?
收费.顾客到哪家商场购物花费少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】周末,小华和小亮想用所学的数学知识测量家门前小河的宽.测量时,他们选择了河对岸边的一棵大树,将其底部作为点A,在他们所在的岸边选择了点B,使得AB与河岸垂直,并在B点竖起标杆BC,再在AB的延长线上选择点D竖起标杆DE,使得点E与点C、A共线.
已知:CB⊥AD,ED⊥AD,测得BC=1m,DE=1.5m,BD=8.5m.测量示意图如图所示.请根据相关测量信息,求河宽AB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店专门销售某种品牌的玩具,成本为30元/件,每天的销售量y(件)与销售单价x(元)之间存在着如图所示的一次函数关系.
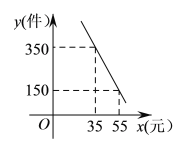
(1)求y与x之间的函数关系式;
(2)当销售单价为多少元时,每天获取的利润最大,最大利润是多少?
(3)为了保证每天的利润不低于3640元,试确定该玩具销售单价的范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
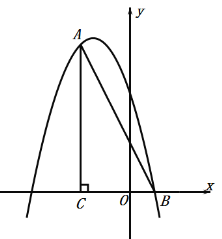
【题目】如图,在平面直角坐标系中,∠ACB=90°,OC=2OB,tan∠ABC=2,点B的坐标为(1,0).抛物线y=﹣x2+bx+c经过A、B两点.
(1)求抛物线的解析式;
(2)点P是直线AB上方抛物线上的一点,过点P作PD垂直x轴于点D,交线段AB于点E,使PE最大.
①求点P的坐标和PE的最大值.
②在直线PD上是否存在点M,使点M在以AB为直径的圆上;若存在,求出点M的坐标,若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com