
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕжаЃЌЁЯACB=90ЁуЃЌOC=2OBЃЌtanЁЯABC=2ЃЌЕуBЕФзјБъЮЊЃЈ1ЃЌ0ЃЉЃЎХзЮяЯпy=Љx2+bx+cОЙ§AЁЂBСНЕуЃЎ
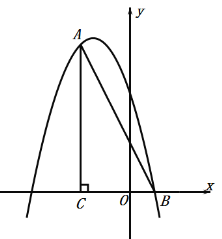
ЃЈ1ЃЉЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧжБЯпABЩЯЗНХзЮяЯпЩЯЕФвЛЕуЃЌЙ§ЕуPзїPDДЙжБxжсгкЕуDЃЌНЛЯпЖЮABгкЕуEЃЌЪЙPEзюДѓЃЎ
ЂйЧѓЕуPЕФзјБъКЭPEЕФзюДѓжЕЃЎ
ЂкдкжБЯпPDЩЯЪЧЗёДцдкЕуMЃЌЪЙЕуMдквдABЮЊжБОЖЕФдВЩЯЃЛШєДцдкЃЌЧѓГіЕуMЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉy=Љx2Љ3x+4ЃЛЃЈ2ЃЉЂй![]() ЃЌP
ЃЌP![]() Ђк MЃЈ
Ђк MЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ
ЁОНтЮіЁП
ЃЈ1ЃЉЯШИљОнвбжЊЧѓЕуAЕФзјБъЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓЖўДЮКЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЂйИљОнAЃЈЉ2ЃЌ6ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌЧѓЕУABЕФНтЮіЪНЮЊЃКy=Љ2x+2ЃЌЩшPЃЈaЃЌЉa2Љ3a+4ЃЉЃЌдђEЃЈaЃЌЉ2a+2ЃЉЃЌРћгУPE=Љa2Љ3a+4Љ(Љ2a+2)=Љ(a+![]() )2+
)2+![]() ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯёгыаджЪМДЧѓНтЃЛ
ЃЌИљОнЖўДЮКЏЪ§ЕФЭМЯёгыаджЪМДЧѓНтЃЛ
ЂкИљОнЕуMдквдABЮЊжБОЖЕФдВЩЯЃЌЕУЕНЁЯAMB=90ЁуЃЌМДAM2+BM2=AB2![]() ЃЌЧѓГі
ЃЌЧѓГі![]() ЃЌ
ЃЌ![]() ЃЌAB2ЙЪПЩСаГіЗНГЬЧѓНт.
ЃЌAB2ЙЪПЩСаГіЗНГЬЧѓНт.
НтЃКЃЈ1ЃЉЁпBЃЈ1ЃЌ0ЃЉ
ЁрOB=1ЃЌ
ЁпOC=2OB=2ЃЌ
ЁрBC=3 ,CЃЈЉ2ЃЌ0ЃЉ
RtЁїABCжаЃЌtanЁЯABC=2ЃЌ
Ёр![]() =2ЃЌ
=2ЃЌ
ЁрAC=6ЃЌ
ЁрAЃЈЉ2ЃЌ6ЃЉЃЌ
АбAЃЈЉ2ЃЌ6ЃЉКЭBЃЈ1ЃЌ0ЃЉДњШыy=Љx2+bx+cЕУЃК![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрХзЮяЯпЕФНтЮіЪНЮЊЃКy=Љx2Љ3x+4ЃЛ
ЃЈ2ЃЉЂйЁпAЃЈЉ2ЃЌ6ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌ
взЕУABЕФНтЮіЪНЮЊЃКy=Љ2x+2ЃЌ
ЩшPЃЈaЃЌЉa2Љ3a+4ЃЉЃЌдђEЃЈaЃЌЉ2a+2ЃЉЃЌ
ЁрPE=Љa2Љ3a+4Љ(Љ2a+2)=Љa2Љa+2=Љ(a+![]() )2+
)2+![]()
ЁрЕБa=![]() ЪБЃЌPE
ЪБЃЌPE![]() =
=![]() ,ДЫЪБP(
,ДЫЪБP(![]() ,
,![]() )
)
ЂкЁпMдкжБЯпPDЩЯЃЌЧвP(![]() ,
,![]() )ЃЌ
)ЃЌ
![]()
Ёр
![]() +
+![]()
AB2=32+62=45ЃЌ
ЁпЕуMдквдABЮЊжБОЖЕФдВЩЯ
ДЫЪБЁЯAMB=90ЁуЃЌ
ЁрAM2+BM2=AB2ЃЌ
Ёр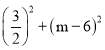 +
+![]() +
+![]() =45
=45
НтЕУЃК![]() ,
,![]()
ЁрMЃЈ![]() ЃЌ
ЃЌ![]() ЃЉЛђЃЈ
ЃЉЛђЃЈ![]() ЃЌ
ЃЌ![]() ЃЉ
ЃЉ


 ЬєеН100ЕЅдЊМьВтЪдОэЯЕСаД№АИ
ЬєеН100ЕЅдЊМьВтЪдОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
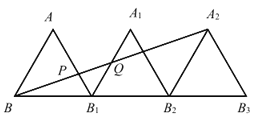
ЁОЬтФПЁПдкRtЁїABCжаЃЌCDЮЊаББпABЩЯЕФИпЃЌAC=3ЃЌBC=4ЃЌЗжБ№гУrЁЂr1ЁЂr2ЁЂБэЪОЁїABCЃЌЁїACDЃЌЁїBCDФкЧадВЕФАыОЖЃЌдђ(ЁЁЁЁ)
A.r+r1+r2=![]() B.r+r1+r2=
B.r+r1+r2=![]()
C.rЉr1Љr2=Љ![]() D.rЉr1Љr2=Љ
D.rЉr1Љr2=Љ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
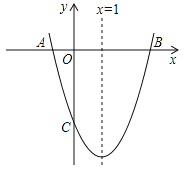
ЁОЬтФПЁПШчЭМЃЌвбжЊХзЮяЯпy=ax2+bx+cЃЈaЁй0ЃЉЕФЖдГЦжсЮЊx=1ЃЌЧвХзЮяЯпОЙ§AЃЈЉ1ЃЌ0ЃЉЁЂCЃЈ0ЃЌЉ3ЃЉСНЕуЃЌгыxжсНЛгкСэвЛЕуBЃЎ
ЃЈ1ЃЉЧѓетЬѕХзЮяЯпЫљЖдгІЕФКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉдкХзЮяЯпЕФЖдГЦжсx=1ЩЯЧѓвЛЕуMЃЌЪЙЕуMЕНЕуAЕФОрРыгыЕНЕуCЕФОрРыжЎКЭзюаЁЃЌВЂЧѓГіДЫЪБЕуMЕФзјБъЃЛ
ЃЈ3ЃЉЩшЕуPЮЊХзЮяЯпЕФЖдГЦжсx=1ЩЯЕФвЛЖЏЕуЃЌЧѓЪЙЁЯPCB=90ЁуЕФЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкЦНУцжБНЧзјБъЯЕxOyжаЃЌвЛДЮКЏЪ§yЃНЉx+2ЕФЭМЯѓгыxжсНЛгкЕуAгыЗДБШР§КЏЪ§![]() ЃЈxЃМ0ЃЉЕФЭМЯѓНЛгкЕуBЃЌЙ§ЕуBзїBCЁЭxжсгкЕуCЃЌЧвOAЃНOCЃЎ
ЃЈxЃМ0ЃЉЕФЭМЯѓНЛгкЕуBЃЌЙ§ЕуBзїBCЁЭxжсгкЕуCЃЌЧвOAЃНOCЃЎ

ЃЈ1ЃЉЧѓЕуAЕФзјБъКЭЗДБШР§КЏЪ§ЕФБэДяЪНЃЛ
ЃЈ2ЃЉШєЕуPЪЧЗДБШР§КЏЪ§![]() ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЕФЕуЃЌЙ§PзїPQЁЮyжсЃЌНЛжБЯпABгкЕуQЃЌЕБPQЃНBCЪБЃЌЧѓЕуPЕФзјБъЃЎ
ЃЈxЃМ0ЃЉЕФЭМЯѓЩЯЕФЕуЃЌЙ§PзїPQЁЮyжсЃЌНЛжБЯпABгкЕуQЃЌЕБPQЃНBCЪБЃЌЧѓЕуPЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпy=ax2+bxЉ![]() ОЙ§ЕуAЃЈ1ЃЌ0ЃЉКЭЕуBЃЈ5ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
ОЙ§ЕуAЃЈ1ЃЌ0ЃЉКЭЕуBЃЈ5ЃЌ0ЃЉЃЌгыyжсНЛгкЕуCЃЎ
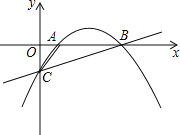
ЃЈ1ЃЉЧѓДЫХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉвдЕуAЮЊдВаФЃЌзїгыжБЯпBCЯрЧаЕФЁбAЃЌЧѓЁбAЕФАыОЖЃЛ
ЃЈ3ЃЉдкжБЯпBCЩЯЗНЕФХзЮяЯпЩЯШЮШЁвЛЕуPЃЌСЌНгPBЃЌPCЃЌЧыЮЪЃКЁїPBCЕФУцЛ§ЪЧЗёДцдкзюДѓжЕЃПШєДцдкЃЌЧѓГіетИізюДѓжЕЕФДЫЪБЕуPЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКВЛЕШЪНзщ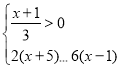
ЃЈ1ЃЉНтетИіВЛЕШЪНзщЃЌОЎАбЫќдкЪ§жсЩЯБэЪОГіРДЃЎ
ЃЈ2ЃЉЙигкxЕФЗжЪНЗНГЬ![]() ЕФНтЪЧВЛЪЧетИіВЛЕШЪНзщЕФећЪ§НтЃП
ЕФНтЪЧВЛЪЧетИіВЛЕШЪНзщЕФећЪ§НтЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
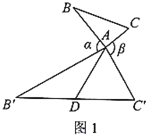
ЁОЬтФПЁПШчЭМ,ШєЙћЁЯ1ЃНЁЯ2ЃЌФЧУДЬэМгЯТСаШЮКЮвЛИіЬѕМўЃКЃЈ1ЃЉ![]() ЃЌЃЈ2ЃЉ
ЃЌЃЈ2ЃЉ![]() ЃЌЃЈ3ЃЉЁЯBЃНЁЯDЃЌЃЈ4ЃЉЁЯCЃНЁЯAEDЃЌ ЦфжаФмХаЖЈЁїABCЁзЁїADEЕФИіЪ§ЮЊ
ЃЌЃЈ3ЃЉЁЯBЃНЁЯDЃЌЃЈ4ЃЉЁЯCЃНЁЯAEDЃЌ ЦфжаФмХаЖЈЁїABCЁзЁїADEЕФИіЪ§ЮЊ

A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЁїA2B2B3 ЪЧШЋЕШЕФЕШБпШ§НЧаЮЃЌЕу BЃЌB1ЃЌB2ЃЌB3 дкЭЌвЛЬѕ жБЯпЩЯЃЌСЌНг A2B НЛ AB1 гкЕу PЃЌНЛ A1B1 гкЕу QЃЌдђ PB1ЁУQB1 ЕФжЕЮЊ___ЃЎ
ЃЌЁїA2B2B3 ЪЧШЋЕШЕФЕШБпШ§НЧаЮЃЌЕу BЃЌB1ЃЌB2ЃЌB3 дкЭЌвЛЬѕ жБЯпЩЯЃЌСЌНг A2B НЛ AB1 гкЕу PЃЌНЛ A1B1 гкЕу QЃЌдђ PB1ЁУQB1 ЕФжЕЮЊ___ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
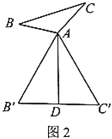
ЁОЬтФПЁПЖЈвхЃКШчЭМ1ЃЌдк![]() жаЃЌАб
жаЃЌАб![]() ШЦЕу
ШЦЕу![]() ФцЪБеыа§зЊ
ФцЪБеыа§зЊ![]() ЃЈ
ЃЈ![]() ЃЉВЂбгГЄвЛБЖЕУЕН
ЃЉВЂбгГЄвЛБЖЕУЕН![]() ЃЌАб
ЃЌАб![]() ШЦЕу
ШЦЕу![]() ЫГЪБеыа§зЊ
ЫГЪБеыа§зЊ![]() ВЂбгГЄвЛБЖЕУЕН
ВЂбгГЄвЛБЖЕУЕН![]() ЃЌСЌНг
ЃЌСЌНг![]() ЃЎЕБ
ЃЎЕБ![]() ЪБЃЌГЦ
ЪБЃЌГЦ![]() ЪЧ
ЪЧ![]() ЕФЁАБЖа§Ш§НЧаЮЁБЃЌ
ЕФЁАБЖа§Ш§НЧаЮЁБЃЌ![]() Бп
Бп![]() ЩЯЕФжаЯп
ЩЯЕФжаЯп![]() Назі
Назі![]() ЕФЁАБЖа§жаЯпЁБЃЎ
ЕФЁАБЖа§жаЯпЁБЃЎ
ЬиР§ИажЊЃК
ЃЈ1ЃЉШчЭМ1ЃЌЕБ![]() ЃЌ
ЃЌ![]() ЪБЃЌдђЁАБЖа§жаЯпЁБ
ЪБЃЌдђЁАБЖа§жаЯпЁБ![]() ГЄЮЊ______ЃЛШчЭМ2ЃЌЕБ
ГЄЮЊ______ЃЛШчЭМ2ЃЌЕБ![]() ЮЊЕШБпШ§НЧаЮЪБЃЌЁАБЖа§жаЯпЁБ
ЮЊЕШБпШ§НЧаЮЪБЃЌЁАБЖа§жаЯпЁБ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЮЊ______ЃЛ
ЕФЪ§СПЙиЯЕЮЊ______ЃЛ
ВТЯыТлжЄЃК
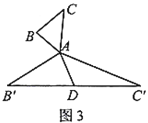
ЃЈ2ЃЉдкЭМ3жаЃЌЕБ![]() ЮЊШЮвтШ§НЧаЮЪБЃЌВТЯыЁАБЖа§жаЯпЁБ
ЮЊШЮвтШ§НЧаЮЪБЃЌВТЯыЁАБЖа§жаЯпЁБ![]() гы
гы![]() ЕФЪ§СПЙиЯЕЃЌВЂИјгшжЄУїЃЎ
ЕФЪ§СПЙиЯЕЃЌВЂИјгшжЄУїЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com