
����Ŀ����ͼ������ֽ�е�ÿ��С�����DZ߳�Ϊ1����λ�������Σ��ڽ���ƽ��ֱ������ϵ����ABC�Ķ�����ڸ���ϣ���B������Ϊ��1��0����
��1��������ABC����x��ԳƵ���A1B1C1��
��2����������ABC��ԭ��O����ʱ����ת90�����õ���A2B2C2����д����C2�����ꣻ
��3����A1B1C1����A2B2C2�����ĶԳ����������ĶԳƣ�д���Գ����ĵ����꣮
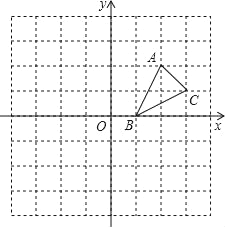
���𰸡���1������������2������������C2������Ϊ��1��3������3����A1B1C1����A2B2C2�����ĶԳƣ��Գ�����Ϊ��![]() ��
��![]() ��
��
��������
(1)����A��B��C����x��ĶԳƵ㣬Ȼ��˳�����Ӽ��ɵõ�;
(2)��A��B��C��ԭ�㰴��ʱ����ת90�ȵõ���Ӧ�㣬Ȼ��˳�����Ӽ��ɵõ�������ͼ��д��C2������;
(3)�����ĶԳƣ��������ԳƵ㣬���ߵĽ�����ǶԳ����ģ��Ӷ������ҳ��Գ����ĵ�����.
��1����ͼ��ʾ����A1B1C1��Ϊ����
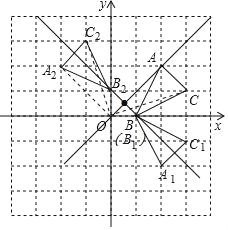
��2����ͼ��ʾ����A2B2C2��Ϊ����C2������Ϊ��1��3����
��3����A1B1C1����A2B2C2�����ĶԳƣ��Գ�����Ϊ��![]() ��
��![]() ����
����



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ȫ�ȵĵ���ֱ�������Σ�б�߳�Ϊ2������ͼ���ã�����һ��������45���ǵ��������һ�������ε�ֱ�Ƕ���A�غϣ���������ABC�̶�������һ���������Ƶ�A��תʱ�����ĽDZߺ�б�����ڵ�ֱ�߷ֱ����BC���ڵ�E��F����BF=![]() CE=
CE=![]() ��
��![]() ����
����![]() �ĺ���ͼ������ǣ� ��
�ĺ���ͼ������ǣ� ��
A.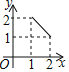 B.
B.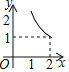 C.
C.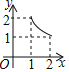 D.
D.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
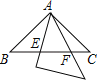
����Ŀ����ͼ1���������ABC�У�D��E�ֱ���AB��BC���е㣬��F��AC�ϣ��������AFE=��A��DM��EF��AC�ڵ�M.
��1��֤����DM=DA��
��2����ͼ2����G��BE�ϣ��ҡ�BDG=��C����֤����DEG�ס�ECF��
��3����ͼ2�У�ȡCE��һ��H��ʹ�á�CFH=��B����BG=3����EH�ij�.
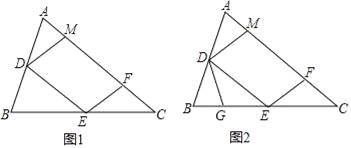
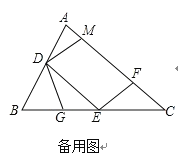
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����壺�����������һ���ϵ����߳�ǡ�õ�����ߵij�����ô�����������Ϊ���������������������߳�Ϊ�������������������߳�Ϊ��������������
���⣺��1��������ͼ���л�һ����ABΪ�����ߵĺ��������Σ�ʹ����������C���ڸ���ϣ�
 ����������
����������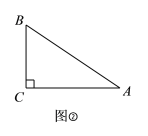
��2����ͼ�ڣ���Rt��ABC�У���C=90����![]() ����֤����ABC������������������
����֤����ABC������������������
���ã���3����֪��������ABC������������������AB=AC=20����ױ�BC�ij�����ͼ��𣩣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���κ���y=ax2+bx+c��a��0���е�x��y�����±���
x | �� | 0 | 1 | 2 | 3 | 4 | 5 | �� |
y | �� | 3 | 0 | ��1 | 0 | m | 8 | �� |
��1�������m��ֵΪ________��
��2��������ϵ�����ú�����ͼ��
��3����y��0ʱ��x��ȡֵ��ΧΪ_____________

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ����в��ϣ�
��֪ʵ��m��n����(2m2��n2��1)(2m2��n2��1)��80������2m2��n2��ֵ.
�⣺��2m2��n2��t����ԭ���̱�Ϊ(t��1)(t��1)��80��������t2��1��80��t2��81��
����t����9����Ϊ2m2��n2��0������2m2��n2��9.
�������ַ�����Ϊ����Ԫ������������ijЩ���ֿ���һ�����ݣ���������ĸ����(����Ԫ)������ʹ���ӵ������.
���������Ķ��������ݣ�����������⣬��д��������.
��1����֪ʵ��x��y������(2x2��2y2��3)(2x2��2y2��3)��27����x2��y2��ֵ.
��2����֪Rt��ACB������Ϊa��b��c��cΪб�ߣ�������a��b����(a2��b2)(a2��b2��4)��5����Rt��ACB���Բ�İ뾶��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���׳���A�ص�B�أ��ҳ���B�ص�A�أ��ҳ��ȳ����ȵ����������֮��ľ���y��ǧ�ף�����ʻ��ʱ��x��Сʱ���ĺ�����ϵ��ͼ��ʾ��������˵���в���ȷ���ǣ�������
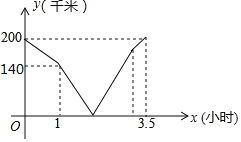
A.�׳����ٶ���80km/hB.�ҳ����ٶ���60km/h
C.�׳�����1h���ҳ�����D.�ҳ�����Ŀ�ĵ�ʱ�׳��� B��10km
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD�У���OΪ����ԭ�㣬��B������Ϊ(4��3)����A��C���������ϣ���P��BC���ϣ�ֱ��11��y=2x+3��ֱ��12��y=2x��3��
��1���ֱ���ֱ��11��x�ᡢֱ��12��AB�Ľ���D��E�����ꣻ
��2����֪��M�ھ���ABCD�ڲ�������ֱ��12�ϵĵ㣬����APM�ǵ���ֱ�������Σ����M�����ꣻ
��3�����ǰ�ֱ��11��ֱ��12�ϵĵ�����ɵ�ͼ�γ�Ϊͼ��F����֪����ANPQ�Ķ���N��ͼ��F�ϣ�����AP���Ϸ���Q������ƽ���ڵĵ㣬��N��ĺ�����Ϊx����ֱ��д��x��ȡֵ��Χ(����˵������)��
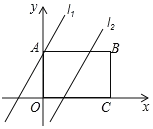
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪���ı���ABCD�У�![]() ��
��![]() ��AD=CD���Խ���AC��BD�ཻ�ڵ�O����BDƽ�֡�ABC������A��
��AD=CD���Խ���AC��BD�ཻ�ڵ�O����BDƽ�֡�ABC������A��![]() ������ΪH.
������ΪH.
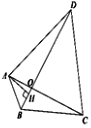
(1)��֤��![]() ��
��
(2)�ж��߶�BH��DH��BC֮���������ϵ����֤��.
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com