
ΓΨΧβΡΩΓΩΕ®“εΘΚ»γΙϊ»ΐΫ«–Έ”–“Μ±Ώ…œΒΡ÷–œΏ≥Λ«ΓΚΟΒ»”Ύ’β±ΏΒΡ≥ΛΘ§Ρ«Ο¥≥Τ’βΗω»ΐΫ«–ΈΈΣΓΑΚΆΟά»ΐΫ«–ΈΓ±Θ§’βΧθ±Ώ≥ΤΈΣΓΑΚΆΟά±ΏΓ±Θ§’βΧθ÷–œΏ≥ΤΈΣΓΑΚΆΟά÷–œΏΓ±Θ°
άμΫβΘΚΘ®1Θ©«κΡψ‘ΎΆΦΔΌ÷–Μ≠“ΜΗω“‘ABΈΣΚΆΟά±ΏΒΡΚΆΟά»ΐΫ«–ΈΘ§ ΙΒΎ»ΐΗωΕΞΒψC¬δ‘ΎΗώΒψ…œΘΜ
 ΓΓΓΓΓΓΓΓΓΓ
ΓΓΓΓΓΓΓΓΓΓ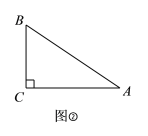
Θ®2Θ©»γΆΦΔΎΘ§‘ΎRtΓςABC÷–Θ§ΓœC=90ΓψΘ§![]() Θ°«σ÷ΛΘΚΓςABC «ΓΑΚΆΟά»ΐΫ«–ΈΓ±Θ°
Θ°«σ÷ΛΘΚΓςABC «ΓΑΚΆΟά»ΐΫ«–ΈΓ±Θ°
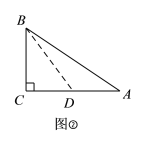
‘Υ”ΟΘΚΘ®3Θ©“―÷ΣΘ§Β»―ϋΓςABC «ΓΑΚΆΟά»ΐΫ«–ΈΓ±Θ§AB=AC=20Θ§«σΒΉ±ΏBCΒΡ≥ΛΘ®Μ≠ΆΦΫβ¥πΘ©Θ°
ΓΨ¥πΑΗΓΩΘ®1Θ©»γΆΦΘΜΦϊΫβΈωΘΜΘ®2Θ©ΦϊΫβΈωΘΜΘ®3Θ©ΒΉ±ΏBCΒΡ≥ΛΈΣ![]() Μρ
Μρ![]() Θ°
Θ°
ΓΨΫβΈωΓΩ
Θ®1Θ©ΗυΨίΓΑΚΆΟά»ΐΫ«–ΈΓ±ΒΡΕ®“εΜ≠≥ωΆΦ–ΈΦ¥Ω…Θ°
Θ®2Θ©»γΆΦΔΎΘ§ΗυΨίΕ®“εRtΓςABC÷–Θ§ΚΆΟά÷–œΏ“ΜΕ® «Ϋœ≥Λ÷±Ϋ«±Ώ…œΒΡ÷–œΏΘ°ΗυΨίΓΑΚΆΟά»ΐΫ«–ΈΓ±ΒΡΕ®“ε÷ΛΟςΦ¥Ω…Θ°
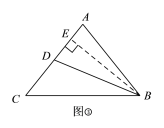
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚ»γΆΦΔέΘ§Β±―ϋ…œΒΡ÷–œΏBD=AC ±Θ§‘ρAB=BDΘ§ΙΐBΉςBEΓΆAD”ΎEΘ°»γΆΦΔήΘ§Β±ΒΉ±Ώ…œΒΡ÷–œΏAD=BC ±Θ§‘ρADΓΆBCΘ§«“AD=2BDΘ§Ζ÷±π«σΫβΦ¥Ω…ΫβΨωΈ ΧβΘ°
Θ®1Θ©»γΆΦΘΜ

Θ®2Θ©÷ΛΟςΘΚ»γΆΦΔΎΘ§
ΗυΨίΕ®“εΘ§
RtΓςABC÷–Θ§
ΚΆΟά÷–œΏ“ΜΕ® «Ϋœ≥Λ÷±Ϋ«±Ώ…œΒΡ÷–œΏΘΜ
»ΓACΒΡ÷–ΒψDΘ§Ν§ΫαBDΘ§
…ηACΘΫ2xΘ§‘ρCDΘΫADΘΫxΘ§
ΓΏ![]() Γύ
Γύ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
‘ΎRtΓςBCD÷–Θ§
![]()
ΓύBDΘΫACΘ§
ΓύΓςABC «ΓΑΚΆΟά»ΐΫ«–ΈΓ±ΘΜ
Θ®3Θ©Ζ÷ΝΫ÷÷«ιΩωΘΚ
»γΆΦΔέΘ§Β±―ϋ…œΒΡ÷–œΏBD=AC ±Θ§‘ρAB=BDΘ§ΙΐBΉςBEΓΆAD”ΎEΘ§
ΓΏAB=AC=20Θ§
ΓύBD=20Θ§
![]() Θ§
Θ§
ΓύCE=10+5=15Θ§
ΓύRtΓςBDE÷–Θ§![]() Θ§
Θ§
ΓύRtΓςBCE÷–Θ§
![]() ΘΜ
ΘΜ
»γΆΦΔήΘ§Β±ΒΉ±Ώ…œΒΡ÷–œΏAD=BC ±Θ§‘ρADΓΆBCΘ§«“AD=2BDΘ§
…ηBD=xΘ§
‘ρ![]() Θ§
Θ§
Γύ![]() Θ§
Θ§
”÷ΓΏxΘΨ0Θ§Γύ![]() Θ§
Θ§
Γύ![]() Θ°
Θ°
Ήέ…œΥυ ωΘ§ΒΉ±ΏBCΒΡ≥ΛΈΣ![]() Μρ
Μρ![]() Θ°
Θ°


 ‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
‘ΡΕΝΩλ≥ΒœΒΝ–¥πΑΗ
| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
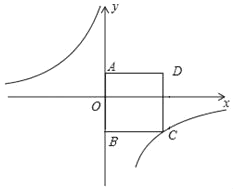
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§ΥΡ±Ώ–ΈABCDΈΣ’ΐΖΫ–ΈΘ§ΒψAΒΡΉχ±ξΈΣΘ®0Θ§3Θ©Θ§ΒψBΒΡΉχ±ξΈΣΘ®0Θ§©¹4Θ©Θ§Ζ¥±»άΐ©¹Κ· ΐyΘΫ![]() Θ®kΓΌ0Θ©ΒΡΆΦœσΨ≠ΙΐΒψCΘ°
Θ®kΓΌ0Θ©ΒΡΆΦœσΨ≠ΙΐΒψCΘ°
Θ®1Θ©«σΖ¥±»άΐΚ· ΐΒΡΫβΈω ΫΘΜ
Θ®2Θ©ΒψP «Ζ¥±»άΐΚ· ΐ‘ΎΒΎΕΰœσœόΒΡΆΦœσ…œΒΡ“ΜΒψΘ§»τΓςPBCΒΡΟφΜΐΒ»”Ύ’ΐΖΫ–ΈABCDΒΡΟφΜΐΘ§«σΒψPΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§÷±œΏy=2x”κΖ¥±»άΐΚ· ΐy=![]() Θ®xΘΨ0Θ©ΒΡΆΦœσΫΜ”ΎΒψAΘ®4Θ§nΘ©Θ§ABΓΆx÷αΘ§¥ΙΉψΈΣBΘ°
Θ®xΘΨ0Θ©ΒΡΆΦœσΫΜ”ΎΒψAΘ®4Θ§nΘ©Θ§ABΓΆx÷αΘ§¥ΙΉψΈΣBΘ°
Θ®1Θ©«σkΒΡ÷ΒΘΜ
Θ®2Θ©ΒψC‘ΎAB…œΘ§»τOC=ACΘ§«σACΒΡ≥ΛΘΜ
Θ®3Θ©ΒψDΈΣx÷α’ΐΑκ÷α…œ“ΜΒψΘ§‘ΎΘ®2Θ©ΒΡΧθΦΰœ¬Θ§»τSΓςOCD=SΓςACDΘ§«σΒψDΒΡΉχ±ξΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
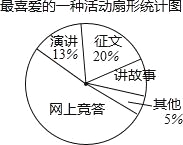
ΓΨΧβΡΩΓΩΫϋΤΎΘ§Έ“ –÷––Γ―ßΙψΖΚΩΣ’ΙΝΥΓΑ¥Ϊ≥–÷–ΜΣΈΡΜ·Θ§Ι≤÷ΰΨΪ…ώΦ“‘ΑΓ±Α°Ιζ÷ς“εΕΝ ιΫΧ”ΐΜνΕ·Θ§Ρ≥÷–―ßΈΣΝΥΫβ―ß…ζΉνœ≤Α°ΒΡΜνΕ·–Έ ΫΘ§“‘ΓΑΈ“Ήνœ≤Α°ΒΡ“Μ÷÷ΜνΕ·Γ±ΈΣ÷ςΧβΘ§Ϋχ––ΥφΜζ≥ι―υΒς≤ιΘ§ ’Φ· ΐΨί’ϊάμΚσΘ§Μφ÷Τ≥ω“‘œ¬ΝΫΖυ≤ΜΆξ’ϊΒΡΆ≥ΦΤΆΦ±μΘ§«κΗυΨίΆΦ÷–ΧαΙ©ΒΡ–≈œΔΘ§Ϋβ¥πœ¬ΟφΒΡΈ ΧβΘΚ
Ήνœ≤Α°ΒΡ“Μ÷÷ΜνΕ·Ά≥ΦΤ±μ
ΜνΕ·–Έ Ϋ | ’ςΈΡ | Ϋ≤Ι ¬ | ―ίΫ≤ | Άχ…œΨΚ¥π | ΤδΥϊ |
»Υ ΐ | 60 | 30 | 39 | a | b |
Θ®1Θ©‘Ύ’β¥Έ≥ι―υΒς≤ι÷–Θ§“ΜΙ≤Βς≤ιΝΥΕύ…ΌΟϊ―ß…ζΘΩ…»–ΈΆ≥ΦΤΆΦ÷–ΓΑΫ≤Ι ¬Γ±≤ΩΖ÷ΒΡ‘≤–ΡΫ« «Εύ…ΌΕ»ΘΩ
Θ®2Θ©»γΙϊ’βΥυ÷–―ßΙ≤”–―ß…ζ3800ΟϊΘ§Ρ«Ο¥«κΡψΙάΦΤΉνœ≤Α°’ςΈΡΜνΕ·ΒΡ―ß…ζ»Υ ΐΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΫΪ±Ώ≥ΛΈΣ6ΒΡ’ΐΖΫ–Έ÷ΫΤ§ABCD―ΊEF’έΒΰ(ΒψEΘ§FΖ÷±π‘Ύ±ΏABΘ§CD…œ)Θ§ ΙΒψB¬δ‘ΎAD±Ώ…œΒΡΒψM¥ΠΘ®ΒψM≤Μ”κAΘ§D÷ΊΘ©Θ§ΒψC¬δ‘ΎΒψN¥ΠΘ§MN”κCDΫΜ”ΎΒψPΘ§ Ν§Ϋ”MBΘ§Β±ΒψM‘Ύ±ΏAD…œ“ΤΕ· ±.”–œ¬Ν–Ϋα¬έΘΚΔΌBM=EFΘΜΔΎ0ΘΦPFΘΦ3 ΘΜΔέΓœAMB=ΓœBMPΘΜΔήΓςPDMΒΡ÷ή≥ΛΥφ÷°ΗΡ±δΘ°Τδ÷–’ΐ»ΖΫα¬έΒΡ–ρΚ≈ «_______Θ°Θ®Α―Ρψ»œΈΣ’ΐ»ΖΒΡΫα¬έΒΡ–ρΚ≈ΕΦΧν…œΘ©

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§’ΐΖΫ–ΈABCDΒΡ±Ώ≥ΛΈΣ1Θ§ΒψA”κ‘≠Βψ÷ΊΚœΘ§ΒψB‘Ύy÷αΒΡ’ΐΑκ÷α…œΘ§ΒψD‘Ύx÷αΒΡΗΚΑκ÷α…œΘ§ΫΪ’ΐΖΫ–ΈABCD»ΤΒψAΡφ ±’κ–ΐΉΣ30Γψ÷Ν’ΐΖΫ–ΈAB'CΓδDΓδΒΡΈΜ÷ΟΘ§B'CΓδ”κCDœύΫΜ”ΎΒψMΘ§‘ρΒψMΒΡΉχ±ξΈΣ_____Θ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
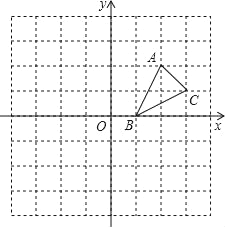
ΓΨΧβΡΩΓΩ»γΆΦΘ§ΖΫΗώ÷Ϋ÷–ΒΡΟΩΗω–ΓΖΫΗώΕΦ «±Ώ≥ΛΈΣ1ΗωΒΞΈΜΒΡ’ΐΖΫ–ΈΘ§‘ΎΫ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΚσΘ§ΓςABCΒΡΕΞΒψΨυ‘ΎΗώΒψ…œΘ§ΒψBΒΡΉχ±ξΈΣΘ®1Θ§0Θ©Θ°
Θ®1Θ©Μ≠≥ωΓςABCΙΊ”Ύx÷αΕ‘≥ΤΒΡΓςA1B1C1ΘΜ
Θ®2Θ©Μ≠≥ωΫΪΓςABC»Τ‘≠ΒψOΑ¥Ρφ ±’κ–ΐΉΣ90ΓψΥυΒΟΒΡΓςA2B2C2Θ§≤Δ–¥≥ωΒψC2ΒΡΉχ±ξΘΜ
Θ®3Θ©ΓςA1B1C1”κΓςA2B2C2≥…÷––ΡΕ‘≥Τ¬πΘΩ»τ≥…÷––ΡΕ‘≥ΤΘ§–¥≥ωΕ‘≥Τ÷––ΡΒΡΉχ±ξΘ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
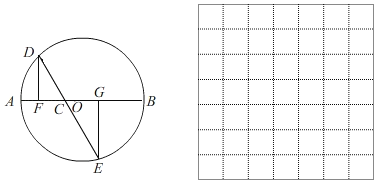
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «Γ―OΒΡ÷±ΨΕΘ§AB=4cmΘ§CΈΣAB…œ“ΜΕ·ΒψΘ§ΙΐΒψCΒΡ÷±œΏΫΜΓ―O”ΎDΓΔEΝΫΒψΘ§«“ΓœACD=60ΓψΘ§DFΓΆAB”ΎΒψFΘ§EGΓΆAB”ΎΒψGΘ§Β±ΒψC‘ΎAB…œ‘ΥΕ· ±Θ§…ηAF=xcmΘ§DE=ycm(Β±xΒΡ÷ΒΈΣ0Μρ3 ±Θ§yΒΡ÷ΒΈΣ2)Θ§ΧΫΨΩΚ· ΐyΥφΉ‘±δΝΩxΒΡ±δΜ·Εχ±δΜ·ΒΡΙφ¬…Θ°
Θ®1Θ©Ά®Ιΐ»ΓΒψΓΔΜ≠ΆΦΓΔ≤βΝΩΘ§ΒΟΒΫΝΥx”κyΒΡΦΗΉιΕ‘”Π÷ΒΘ§»γœ¬±μΘΚ
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
Θ®2Θ©Ϋ®ΝΔΤΫΟφ÷±Ϋ«Ήχ±ξœΒΘ§Οη≥ω“‘≤Ι»ΪΚσΒΡ±μ÷–ΗςΕ‘Ε‘”Π÷ΒΈΣΉχ±ξΒΡΒψΘ§Μ≠≥ωΗΟΚ· ΐΒΡΆΦœσΘΜ
Θ®3Θ©ΫαΚœΜ≠≥ωΒΡΚ· ΐΆΦœσΘ§ΫβΨωΈ ΧβΘΚΒψF”κΒψO÷ΊΚœ ±Θ§DE≥ΛΕ»‘ΦΈΣΓΓΓΓΓΓΓΓcm(ΫαΙϊ±ΘΝτ“ΜΈΜ–Γ ΐ)Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘Ύ’ΐΖΫ–Έ![]() ÷–Θ§
÷–Θ§![]() ΈΣ
ΈΣ![]() ±ΏΒΡ÷–ΒψΘ§
±ΏΒΡ÷–ΒψΘ§![]() ΓΔ
ΓΔ![]() Ζ÷±πΈΣ
Ζ÷±πΈΣ![]() ΓΔ
ΓΔ![]() ±Ώ…œΒΡΒψΘ§»τ
±Ώ…œΒΡΒψΘ§»τ![]() Θ§
Θ§![]() Θ§
Θ§![]() Θ§‘ρ
Θ§‘ρ![]() ΒΡ≥ΛΈΣΘ® Θ©
ΒΡ≥ΛΈΣΘ® Θ©
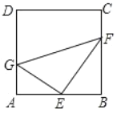
A.2B.3C.![]() D.
D.![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com