
【题目】如图,将边长为6的正方形纸片ABCD沿EF折叠(点E,F分别在边AB,CD上),使点B落在AD边上的点M处(点M不与A,D重),点C落在点N处,MN与CD交于点P, 连接MB,当点M在边AD上移动时.有下列结论:①BM=EF;②0<PF<3 ;③∠AMB=∠BMP;④△PDM的周长随之改变.其中正确结论的序号是_______.(把你认为正确的结论的序号都填上)

【答案】①②③
【解析】
作FG⊥AB于G,证明△ABM≌△GFE(AAS),得出BM=EF,①正确;
若点M与A重合,则C与D重合,P与D重合,PF=3;当M与D重合时,N与C重合,P与C重合,EF与AC重合,CF=0;得出0<PF<3,②正确;
由等腰三角形的性质得出∠ABM=∠EMB,由∠ABC=∠EMN=90°,得出∠AMB=∠BMP,③正确;
可证△AEM∽△DMP,两个三角形的周长的比是AE:MD,设AM=x,根据勾股定理可以用x表示出MD的长与△MAE的周长,根据周长的比等于相似比,求出△PDM的周长=12为定值,得出④不正确,即可得出结论.
解:作FG⊥AB于G,如图所示:
则∠EGF=90°,GF=BC=AB,
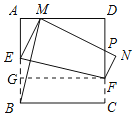
∵四边形ABCD是正方形,
∴∠ABC=∠A=90°,
∴∠ABM+∠AMB=90°,
由折叠的性质得:BM⊥EF,BE=ME,∠EMN=∠ABC=90°,
∴∠ABM+∠GEF=∠ABM+∠AMB=90°,
∴∠AMB=∠GEF,
在△ABM和△GFE中,
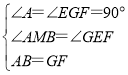 ,
,
∴△ABM≌△GFE(AAS),
∴BM=EF,①正确;
若点M与A重合,则C与D重合,P与D重合,PF=3;
当M与D重合时,N与C重合,P与C重合,EF与AC重合,CF=0;
∵点M不与A,D重合,
∴0<PF<3,②正确;
∵BE=ME,
∴∠ABM=∠EMB,
∵∠ABC=∠EMN=90°,
∴∠AMB=∠BMP,③正确;
设AM=x,则MD=6-x.
由折叠性质可知,EM=BE=6-AE,
在Rt△AEM中,AE2+AM2=EM2,即AE2+x2=(6-AE)2,
整理得:AE2+x2=36-12AE+AE2,
∴AE=![]() (36-x2),
(36-x2),
又∵∠EMP=90°,
∴∠AME+∠DMP=90°.
∵∠AME+∠AEM=90°,
∴∠AEM=∠DMP.
又∵∠A=∠D,
∴△PDM∽△MAE.
∴![]() ,
,
∴△PDM的周长=△MAE的周长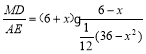 =12.
=12.
∴△PDM的周长保持不变,④不正确;
故答案为:①②③.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B-A-D-C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
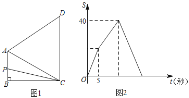
A. 10B. ![]() C. 8D.
C. 8D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某同学练习推铅球,铅球推出后在空中飞行的轨迹是一条抛物线,铅球在离地面1米高的A处推出,达到最高点B时的高度是2.6米,推出的水平距离是4米,铅球在地面上点C处着地
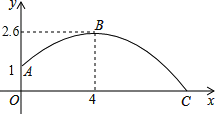
(1)根据如图所示的直角坐标系求抛物线的解析式;
(2)这个同学推出的铅球有多远?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在锐角△ABC中,D、E分别是AB、BC的中点,点F在AC上,且满足∠AFE=∠A,DM∥EF交AC于点M.
(1)证明:DM=DA;
(2)如图2,点G在BE上,且∠BDG=∠C,求证:△DEG∽△ECF;
(3)在图2中,取CE上一点H,使得∠CFH=∠B,若BG=3,求EH的长.
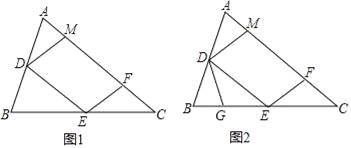
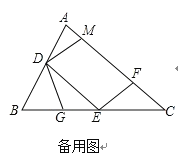
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线l1的解析式为y=﹣3x+3,且l1与x轴交于点D,直线l2经过点A、B,直线l1、l2交于点C.
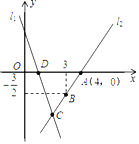
(1)求直线l2的解析表达式;
(2)求△ADC的面积;
(3)在直线l2上存在异于点C的另一点P,使得△ADP与△ADC的面积相等,请求出点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如果三角形有一边上的中线长恰好等于这边的长,那么称这个三角形为“和美三角形”,这条边称为“和美边”,这条中线称为“和美中线”.
理解:(1)请你在图①中画一个以AB为和美边的和美三角形,使第三个顶点C落在格点上;

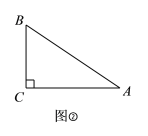
(2)如图②,在Rt△ABC中,∠C=90°,![]() .求证:△ABC是“和美三角形”.
.求证:△ABC是“和美三角形”.
运用:(3)已知,等腰△ABC是“和美三角形”,AB=AC=20,求底边BC的长(画图解答).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数y=ax2+bx+c(a≠0)中的x和y满足下表:
x | … | 0 | 1 | 2 | 3 | 4 | 5 | … |
y | … | 3 | 0 | -1 | 0 | m | 8 | … |
(1)可求得m的值为________;
(2)在坐标系画出该函数的图象;
(3)当y≥0时,x的取值范围为_____________

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲车从A地到B地,乙车从B地到A地,乙车先出发先到达,甲乙两车之间的距离y(千米)与行驶的时间x(小时)的函数关系如图所示,则下列说法中不正确的是( )
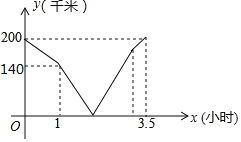
A.甲车的速度是80km/hB.乙车的速度是60km/h
C.甲车出发1h与乙车相遇D.乙车到达目的地时甲车离 B地10km
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小王是“新星厂”的一名工人,请你阅读下列信息:
信息一:工人工作时间:每天上午8:00—12:00,下午14:00—18:00,每月工作25天;
信息二:小王生产甲、乙两种产品的件数与所用时间的关系见下表:
生产甲种产品数(件) | 生产乙种产品数(件) | 所用时间(分钟) |
10 | 10 | 350 |
30 | 20 | 850 |
信息三:按件计酬,每生产一件甲种产品得1.50元,每生产一件乙种产品得2.80元;
信息四:该厂工人每月收入由底薪和计酬工资两部分构成,小王每月的底薪为1900元.请根据以上信息,解答下列问题:
(1)小王每生产一件甲种产品和一件乙种产品分别需要多少分钟;
(2)2018年1月工厂要求小王生产甲种产品的件数不少于60件,则小王该月收入最多是多少元?此时小王生产的甲、乙两种产品分别是多少件?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com