
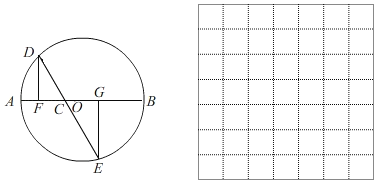
【题目】如图,AB是⊙O的直径,AB=4cm,C为AB上一动点,过点C的直线交⊙O于D、E两点,且∠ACD=60°,DF⊥AB于点F,EG⊥AB于点G,当点C在AB上运动时,设AF=xcm,DE=ycm(当x的值为0或3时,y的值为2),探究函数y随自变量x的变化而变化的规律.
(1)通过取点、画图、测量,得到了x与y的几组对应值,如下表:
x/cm | 0 | 0.40 | 0.55 | 1.00 | 1.80 | 2.29 | 2.61 | 3 |
y/cm | 2 | 3.68 | 3.84 | 3.65 | 3.13 | 2.70 | 2 |
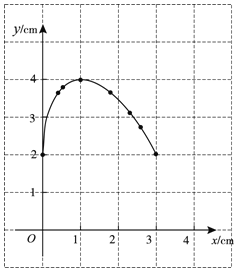
(2)建立平面直角坐标系,描出以补全后的表中各对对应值为坐标的点,画出该函数的图象;
(3)结合画出的函数图象,解决问题:点F与点O重合时,DE长度约为 cm(结果保留一位小数).
【答案】(1)4.00;(2)答案见解析;(3)3.5.
【解析】
(1)先求出OF=1,利用勾股定理求出DF,进而求出∠ODF=30°,进而判断出DE过点O即可求解;
(2)利用画函数图象的方法即可得出结论;
(3)先作出图形,进而求出OD=2,利用锐角三角函数求出DM,即可得出DE=![]() ,即可得出结论.
,即可得出结论.
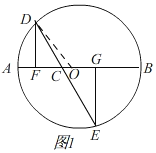
(1)如图1,(为了说明点C和点O重合,DE没画成过点O)
连接OD,当x=1时,AF=1.
∵OA=2,
∴OF=OA﹣AF=1.
∵DF⊥AB,
∴∠DFO=90°,
在Rt△OFD中,OD=2,OF=1,
根据勾股定理得:DF![]() ,
,
∴tan∠ODF![]() ,
,
∴∠ODF=30°,
在Rt△CFD中,∠ACD=60°,
∴∠CDF=30°,
∴∠CDF=∠ODF,
∴DE过点O,
∴DE是⊙O的直径,
∴DE=2OD=4,
∴y=4.
故答案为:4.00;
(2)描点,连线,得出函数图象如右图所示;
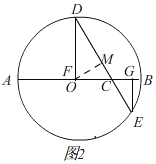
(3)如图2.
∵点F和点O重合,
∴OD=OA=2,
过点O作OM⊥DE于M,
∴DE=2DM.
∵∠ACD=60°,
∴∠ODE=90°﹣∠ACD=30°,
在Rt△OMD中,cos∠ODE![]() ,
,
∴DM=ODcos∠ODE=2×cos30°![]() ,
,
∴DE=2DM=2![]() 3.5.
3.5.
故答案为:3.5.


 优等生题库系列答案
优等生题库系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=4,以AB为直径的⊙O交BC于点D,交AC于点E,点P是AB的延长线上一点,且∠PDB=![]() ∠A,连接DE,OE.
∠A,连接DE,OE.
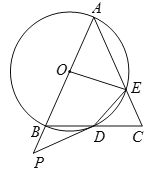
(1)求证:PD是⊙O的切线.
(2)填空:①当∠P的度数为______时,四边形OBDE是菱形;
②当∠BAC=45°时,△CDE的面积为_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,EF,EB是⊙O的弦,且EF=EB,EF与AB交于点C,连接OF,若∠AOF=40°,则∠F的度数是( )
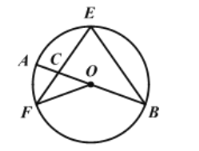
A.20°B.35°C.40°D.55°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】学校准备在各班设立图书角以丰富同学们的课余文化生活.为了更合理的搭配各类书籍,学校团委以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图①和图②提供的信息,解答下列问题:
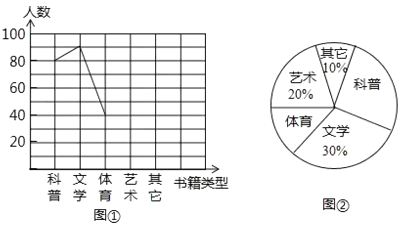
(1)在这次抽样调查中,一共调查了_____________名学生;
(2)请把折线统计图补充完整;
(3)在统计图②中,求出“体育”部分所对应的圆心角的度数;
(4)若该校有学生2400人,估计喜欢“科普”书籍的有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小明同学设计的“过圆外一点作圆的切线”的尺规作图的过程.
已知:如图1,![]() 和
和![]() 外的一点
外的一点![]() .
.
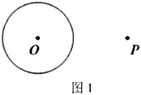
求作:过点![]() 作
作![]() 的切线.
的切线.
作法:如图2,
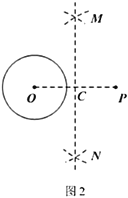
①连接![]() ;
;
②作线段![]() 的垂直平分线
的垂直平分线![]() ,直线
,直线![]() 交
交![]() 于
于![]() ;
;
③以点![]() 为圆心,
为圆心,![]() 为半径作圆,交
为半径作圆,交![]() 于点
于点![]() 和
和![]() ;
;
④作直线![]() 和
和![]() .
.
则![]() ,
,![]() 就是所求作的
就是所求作的![]() 的切线.
的切线.
根据上述作图过程,回答问题:
(1)用直尺和圆规,补全图2中的图形;
(2)完成下面的证明:
证明:连接![]() ,
,![]() ,
,
∵由作图可知![]() 是
是![]() 的直径,
的直径,
∴![]() (______)(填依据),
(______)(填依据),
∴![]() ,
,![]() ,
,
又∵![]() 和
和![]() 是
是![]() 的半径,
的半径,
∴![]() ,
,![]() 就是
就是![]() 的切线(______)(填依据).
的切线(______)(填依据).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了了解学生使用手机情况,随机抽取了部分学生进行|使用手机的目的和每周使用手机的时间的问卷调查,并绘制成如图所示的统计图,已知“查资料”的人数为38人。
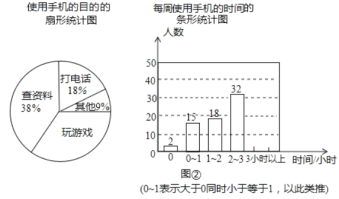
根据以上信息,回答下列问题:
(1)这次调查中,一共抽查了__________名学生;
(2)在扇形统计图中,“玩游戏”所对应的圆心角的度数是___________度;
(3)补全条形统计图;
(4)若该校共有学生2000人,请你估计每周使用手机时间超过2小时的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是 ( )
A.要调查现在人们在数学化时代的生活方式,宜采用普查方式
B.一组数据3,4,4,6,8,5的中位数是4
C.必然事件的概率是100%,随机事件的概率大于0而小于1
D.若甲组数据的方差![]() =0.128,乙组数据的方差
=0.128,乙组数据的方差![]() =0.036,则甲组数据更稳定
=0.036,则甲组数据更稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的边长为4,点E,F分别在边AB,AD上,且∠ECF=45°,CF的延长线交BA的延长线于点G,CE的延长线交DA的延长线于点H,连接AC,EF.,GH.
(1)填空:∠AHC ∠ACG;(填“>”或“<”或“=”)
(2)线段AC,AG,AH什么关系?请说明理由;
(3)设AE=m,
①△AGH的面积S有变化吗?如果变化.请求出S与m的函数关系式;如果不变化,请求出定值.
②请直接写出使△CGH是等腰三角形的m值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在菱形ABCD中,∠BAD=120°,AB=4cm.动点E在射线BC上匀速运动,其运动速度为1cm/s,运动时间为ts.连接AE,并将线段AE绕点A顺时针旋转120°至AF,连接BF.
(1)试说明无论t为何值,△ABF的面积始终为定值,并求出该定值;
(2)如图2,连接EF,BD,交于点H,BD与AE交于点G,当t为何值时,△HEG为直角三角形?
(3)如图3、当F、B、D三点共线时,求tan∠FEB的值.
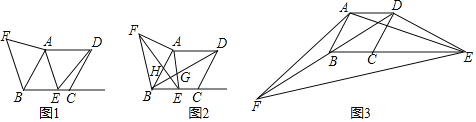
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com