
分析 (1)先按照去括号法则去掉整式中的小括号,再合并整式中的同类项即可;
(2)先将A=2x2-3xy+2y2,B=2x2+xy-3y2代入3A-2B,再去括号、合并同类项即可.
解答 解:(1)a3b+(a3b-2c)-2(a3b-c)
=a3b+a3b-2c-2a3b+2c
=0;
(2)∵A=2x2-3xy+2y2,B=2x2+xy-3y2,
∴3A-2B=3(2x2-3xy+2y2)-2(2x2+xy-3y2)
=6x2-9xy+6y2-4x2-2xy+6y2
=2x2-11xy+12y2.
点评 本题考查了整式的加减、去括号法则两个考点.解决此类题目的关键是熟记去括号法则,熟练运用合并同类项的法则,这是各地中考的常考点.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
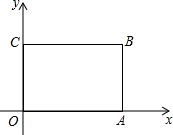 如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点O为位似中心,矩形OABC的位似图形O′A′B′C′,使它的面积等于矩形OABC面积的$\frac{1}{4}$,并分别写出点A′,B′,C′的坐标.
如图,矩形OABC的顶点坐标分别为O(0,0)、A(6,0)、B(6,4)、C(0,4),画出以点O为位似中心,矩形OABC的位似图形O′A′B′C′,使它的面积等于矩形OABC面积的$\frac{1}{4}$,并分别写出点A′,B′,C′的坐标.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
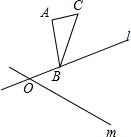 如图,直线1和m相交于点O
如图,直线1和m相交于点O查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com