
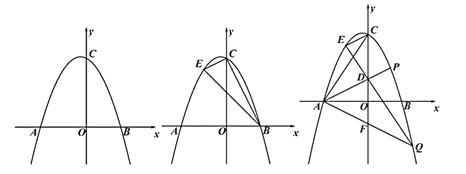
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴正半轴于
轴正半轴于![]() ,且
,且![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)![]() 是第二象限抛物线上一点,坐标为
是第二象限抛物线上一点,坐标为![]() ,连接
,连接![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() 并延长交抛物线与点
并延长交抛物线与点![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,将点
,将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() 连接
连接![]() ,若
,若![]() 轴,求Q点坐标.
轴,求Q点坐标.
【答案】(1)![]() ,
,![]() ;
;
(2)![]() ;
;
(3)![]() ;
;
【解析】
(1)根据二次函数的解析式可以先确定对称轴为:![]() ,所以结合二次函数的对称性即可确定
,所以结合二次函数的对称性即可确定![]() 两点的坐标;
两点的坐标;
(2)根据(1)中求出的![]() 两点坐标可以将二次函数表示为
两点坐标可以将二次函数表示为![]() ,进一步化简可以得到
,进一步化简可以得到![]() ,那么
,那么![]() 点的坐标就可以表示为
点的坐标就可以表示为![]() ,将
,将![]() 点的坐标代入二次函数的解析式即可解出
点的坐标代入二次函数的解析式即可解出![]() ,从而求得
,从而求得![]() 点和
点和![]() 点的坐标,利用铅锤高即可求出
点的坐标,利用铅锤高即可求出![]() 的面积;
的面积;
(3)首先根据题意作出点![]() ,并分别过点
,并分别过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴,结合二次函数的解析式设出
轴,结合二次函数的解析式设出![]() ,求出直线
,求出直线![]() 的解析式,再进一步求出直线
的解析式,再进一步求出直线![]() 的解析式,根据直线和抛物线的交点问题求出含参数的
的解析式,根据直线和抛物线的交点问题求出含参数的![]() 坐标,然后结合相似三角形确定
坐标,然后结合相似三角形确定![]() 坐标,即可求解;
坐标,即可求解;
(1)![]() 二次函数的解析式为:
二次函数的解析式为:![]()
![]() 二次函数的对称轴为:
二次函数的对称轴为:![]()
![]()
![]()
![]()
![]() ,
,![]()
(2)由(1)得![]() ,
,![]()
![]() 二次函数得解析式为:
二次函数得解析式为:![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
把![]() 点代入二次函数解析式
点代入二次函数解析式![]() 可得:
可得:![]()
化简得:![]()
解得:![]() (舍)
(舍)
![]()
![]()
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 的解析式为:
的解析式为:![]()
将![]() 两点代入可得:
两点代入可得:![]()
![]() 直线
直线![]() 的解析式为:
的解析式为:![]()
![]()
![]()
![]()
![]()
![]()
![]()
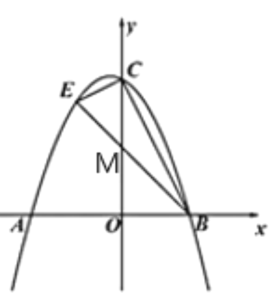
(3)根据题意作出点![]() ,分别过点
,分别过点![]() 作
作![]() 轴,过点
轴,过点![]() 作
作![]() 轴
轴
由(2)可得:![]()
![]() 二次函数的解析式为:
二次函数的解析式为:![]()
设![]() ,直线
,直线![]() 的解析式为:
的解析式为:![]()
将![]() ,
,![]() 两点代入
两点代入![]() 解得:
解得:![]()
![]()
![]()
设直线![]() 的解析式为:
的解析式为:![]()
将![]() ,
,![]() 两点代入
两点代入![]() 解得:
解得:![]()
![]() 直线
直线![]() 与抛物线交于点
与抛物线交于点![]()
![]() 令
令![]()
解得:![]()
![]()
![]() 点的横坐标为
点的横坐标为![]()
![]() 点
点![]() 是由
是由![]() 点绕
点绕![]() 点逆时针旋转
点逆时针旋转![]() 得到
得到
![]()
![]() ,
,![]()
![]()
![]()
![]()
![]() 轴,
轴,![]() 轴
轴
![]()
![]()
![]()
![]()
![]()
在![]() 和
和![]() 中:
中: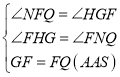
![]()
![]()
![]()
![]()
![]()
![]() 轴
轴
![]()
![]() 点的横坐标为
点的横坐标为![]() ,即
,即![]()
![]()
![]() 轴
轴
![]()
![]()
![]()
![]() ,即
,即![]()
![]()
![]()
![]()
![]()
![]()
![]()
设直线![]() 的解析式为:
的解析式为:![]()
将![]() ,
,![]() 两点代入可得:
两点代入可得:![]()
![]() 直线
直线![]() 与抛物线交于点
与抛物线交于点![]()
![]() 令
令![]()
解得:![]()
![]()
![]() 点的横坐标为
点的横坐标为![]() ,将
,将![]() 代入
代入![]() 可得
可得![]()
![]()
![]()



科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() ,直线
,直线![]() 与抛物线、
与抛物线、![]() 轴分别相交于
轴分别相交于![]() 、
、![]() .
.
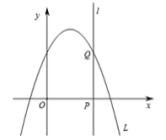
(1)![]() 时,
时,![]() 点的坐标为________;
点的坐标为________;
(2)当![]() 、
、![]() 两点重合时,求
两点重合时,求![]() 的值;
的值;
(3)当![]() 点达到最高时,求抛物线解析式;
点达到最高时,求抛物线解析式;
(4)在抛物线![]() 与
与![]() 轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出
轴所围成的封闭图形的边界上,我们把横坐标是整数的点称为“可点”,直接写出![]() 时“可点”的个数为____.
时“可点”的个数为____.
查看答案和解析>>
科目:初中数学 来源: 题型:
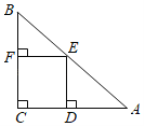
【题目】如图,在直角三角形![]() 中,
中,![]() 是
是![]() 的中点,过点
的中点,过点![]() 作
作![]() 和
和![]() 的垂线,垂足分别为点
的垂线,垂足分别为点![]() 和点
和点![]() ,四边形
,四边形![]() 沿着
沿着![]() 方向以每秒
方向以每秒![]() 个单位的速度匀速运动,点
个单位的速度匀速运动,点![]() 与点
与点![]() 重合时停止运动,设运动时间为
重合时停止运动,设运动时间为![]() ,运动过程中四边形
,运动过程中四边形![]() 与
与![]() 的重叠部分面积为
的重叠部分面积为![]() .则
.则![]() 关于
关于![]() 的函数图象大致为( )
的函数图象大致为( )
A.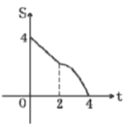 B.
B.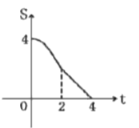
C.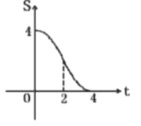 D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着我国经济社会的发展,人民对于美好生活的追求越来越高.某社区为了了解家庭对于文化教育的消费悄况,随机抽取部分家庭,对每户家庭的文化教育年消费金额进行问卷调査,根据调查结果绘制成两幅不完整的统计图表.
请你根据统计图表提供的信息,解答下列问题:
组別 | 家庭年文化教育消费金额x(元) | 户数 |
A | x≤5000 | 36 |
B | 5000<x≤10000 | m |
C | 10000<x≤15000 | 27 |
D | 15000<x≤20000 | 15 |
E | x>20000 | 30 |
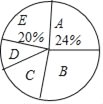
(1)本次被调査的家庭有__________户,表中 m=__________;
(2)本次调查数据的中位数出现在__________组.扇形统计图中,D组所在扇形的圆心角是__________度;
(3)这个社区有2500户家庭,请你估计家庭年文化教育消费10000元以上的家庭有多少户?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、点D为⊙O上两点,线段BC切⊙O于点B,点D在BC的垂直平分线上,CD∥OA,sin∠BCD=![]() ,OA=2BD,若BC=
,OA=2BD,若BC=![]() ,则⊙O的半径为( )
,则⊙O的半径为( )
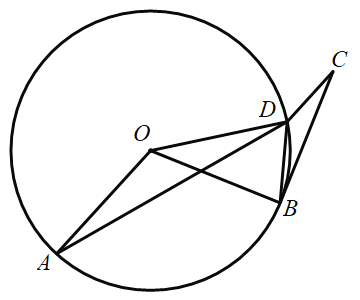
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A在以BC为直径的⊙O上,连接AB、AC,点H为AB的中点.过点H的弦DE⊥BC于点F,连接CD、CH.
(1)求证:AB2=2BC·BF
(2)取AC的中点G,连接HG,过点D作线段DI与AC交于点J,与HJ的延长线交于点I.若AB=AG=4,求DJ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在奉贤创建文明城区的活动中,有两段长度相等的彩色道砖铺设任务,分别交给甲、乙两个施工队同时进行施工.如图是反映所铺设彩色道砖的长度y(米)与施工时间x(时)之间关系的部分图象.请解答下列问题:
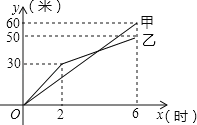
(1)求乙队在2≤x≤6的时段内,y与x之间的函数关系式;
(2)如果甲队施工速度不变,乙队在开挖6小时后,施工速度增加到12米/时,结果两队同时完成了任务.求甲队从开始施工到完工所铺设的彩色道砖的长度为多少米?
查看答案和解析>>
科目:初中数学 来源: 题型:
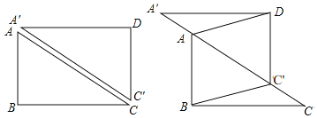
【题目】矩形![]() 中,
中,![]() ,
,![]() ,沿对角线
,沿对角线![]() 将矩形分成两个直角三角形,如图1,其中
将矩形分成两个直角三角形,如图1,其中![]() 不动,
不动,![]() 沿射线
沿射线![]() 的方向以每秒
的方向以每秒![]() 的速度平移,如图2.
的速度平移,如图2.
(1)在平移过程中,当满足什么条件时,四边形![]() 是菱形?说明理由;
是菱形?说明理由;
(2)当四边形![]() 是菱形时,平移了多少秒?
是菱形时,平移了多少秒?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com