
【题目】已知,在![]() 中,
中,![]() ,
,![]() 是
是![]() 上一点,连接
上一点,连接![]() ,
,![]() ,
,![]() ,
,![]() ,则线段
,则线段![]() 的长为__________.
的长为__________.
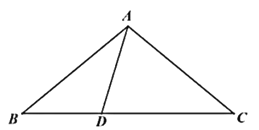
【答案】![]() .
.
【解析】
作∠DAC的角平分线,交BC于点E,作DG⊥AE,DF⊥AB,证明△ABE≌△ACD,假设AB=x,AD=AE=y,根据角平分线定理得到:![]() ,再假设设EG=t,则AG=y-t,多次运用勾股定理以及角平分线的性质即可得到答案;
,再假设设EG=t,则AG=y-t,多次运用勾股定理以及角平分线的性质即可得到答案;
解:如图,作∠DAC的角平分线,交BC于点E,作DG⊥AE,DF⊥AB,
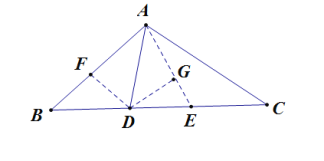
∵![]() ,
,
∴![]() ,
,
又∵AB=AC,
∴∠B=∠C,
∴△ABE≌△ACD(AAS),
∴BE=CD=5,
假设AB=x,AD=AE=y,
根据角平分线定理得到:![]() ,
,
设EG=t,则AG=y-t,
根据勾股定理以及角平分线到角两边的距离相等得到:
![]() ,
,
∴![]() ,
,
又∵![]() ,
,
∴![]() ,
,
在三角形ADG中,![]() ,即:
,即:![]() ,
,
∴![]() ,
,
结合![]() 以及
以及![]() 得到:
得到:
![]() ,即:
,即:![]() ,
,
又∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵x是长度,故是正数,
∴![]() ,
,
故![]() ,
,
故答案是:![]() .
.


 科学实验活动册系列答案
科学实验活动册系列答案科目:初中数学 来源: 题型:
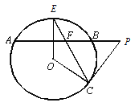
【题目】如图,AB 是⊙O 的弦,半径OE⊥ AB ,P 为 AB 的延长线上一点,PC 与⊙O相切于点 C,连结 CE,交 AB 于点 F,连结 OC.
(1)求证:PC=PF.
(2)连接 BE,若∠CEB=30°,半径为 8,tan P ![]() ,求 FB 的长.
,求 FB 的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市经济技术开发区某智能手机有限公司接到生产300万部智能手机的订单,为了尽快交货,增开了一条生产线,实际每月生产能力比原计划提高了50%,结果比原计划提前5个月完成交货,求每月实际生产智能手机多少万部.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某款篮球架的示意图,支架AC与底座BC所成的∠ACB=65°,支架AB⊥BC,篮球支架HE∥BC,且篮板DF⊥HE于点E,已知底座BC=1米,AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求∠FHE的度数;
(2)已知该款篮球架符合国际篮联规定的篮板下沿D距地面2.90米的规定,求DE的长度.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.41,![]() ≈1.41)
≈1.41)

查看答案和解析>>
科目:初中数学 来源: 题型:
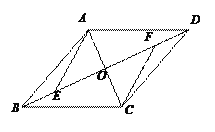
【题目】如图,在□ABCD中,AC、BD相交于点O,点E、F在BD上,且BE=DF.连
接AE、CF.
(1)求证△AOE≌△COF;
(2)若AC⊥EF,连接AF、CE,判断四边形AECF的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
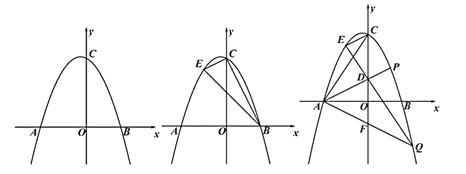
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴正半轴于
轴正半轴于![]() ,且
,且![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)![]() 是第二象限抛物线上一点,坐标为
是第二象限抛物线上一点,坐标为![]() ,连接
,连接![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() 并延长交抛物线与点
并延长交抛物线与点![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,将点
,将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() 连接
连接![]() ,若
,若![]() 轴,求Q点坐标.
轴,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
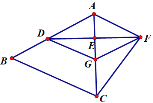
【题目】如图,AB=BC,点D为边AB的中点,点G为AC边的中点,AF∥BC且AD=AF.点E为DF与AC的交点,若AB=6,AE=1,则CF的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 内接于直径为
内接于直径为![]() 的圆,
的圆,![]() .
.
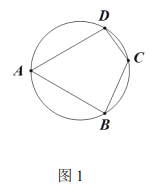
(1)①![]() _ ;
_ ;
②四边形![]() 的周长最大值为_ ;
的周长最大值为_ ;
![]() 如图2,延长
如图2,延长![]() 相交于点
相交于点![]() ,延长
,延长![]() 相交于点
相交于点![]() 求
求![]() 与的
与的![]() 积;
积;
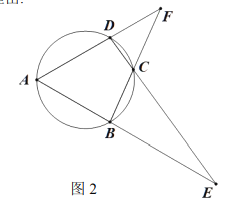
![]() 如图3,连接
如图3,连接![]() 请问在线段
请问在线段![]() 上是否存在点
上是否存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,若存在,请证明;若不存在,请说明理由.
对称,若存在,请证明;若不存在,请说明理由.
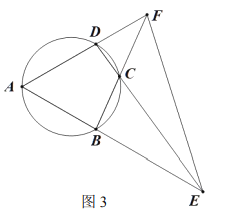
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个三角形的两个内角α,β满足α+2β=90°,那么我们称这样的三角形为“非常三角形”.
(1)若△ABC是“非常三角形”,∠C>90°,∠A=50°,则∠B= .
(2)如图,△ABC中,AB=AC,D是边BC上一点,以BD为直径的⊙O经过点A,连结AD.

①求证:△ADC为“非常三角形”.
②若sinB=![]() ,AB=8,弦AB上是否存在一点P,使得△BDP是“非常三角形”,若存在,请求出线段AP的长度;若不存在,请说明理由.
,AB=8,弦AB上是否存在一点P,使得△BDP是“非常三角形”,若存在,请求出线段AP的长度;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com