
【题目】如图,点A在以BC为直径的⊙O上,连接AB、AC,点H为AB的中点.过点H的弦DE⊥BC于点F,连接CD、CH.
(1)求证:AB2=2BC·BF
(2)取AC的中点G,连接HG,过点D作线段DI与AC交于点J,与HJ的延长线交于点I.若AB=AG=4,求DJ的长.

【答案】(1)证明见解析;(2)![]()
【解析】
(1)直接证明△BFH∽△BAC,得到![]() =
=![]() ,而BH=
,而BH= ![]() ,即可得到结论;
,即可得到结论;
(2)先由cos∠FBH=![]() =
=![]() 得到BF=
得到BF=![]() ,再由勾股定理及线段的和差关系得到DH= HG=
,再由勾股定理及线段的和差关系得到DH= HG=![]() ,再由tan∠HDI=
,再由tan∠HDI=![]() =
=![]() 得到HI=
得到HI=![]() ,从而得到GI,DI,OI的值,又易得△OCJ∽△IGJ,得到
,从而得到GI,DI,OI的值,又易得△OCJ∽△IGJ,得到![]() =
=![]() ,从而得到关键关系:
,从而得到关键关系:![]() ,进而根据DJ=OD+OJ得解.
,进而根据DJ=OD+OJ得解.
解:(1)证明:∵BC为⊙O的直径,DE⊥BC
∴∠BFH=∠BAC=90°
∵∠FBH=∠ABC, 点H为AB的中点
∴△BFH∽△BAC,BH= ![]()
即![]() =
=![]() 即
即![]() =BC·BF
=BC·BF
AB2=2BC·BF
(2)∵点H为AB的中点,点G为AC的中点
∴AH=BH=![]() =
=![]() =2,AC=2AG=8,HG
=2,AC=2AG=8,HG![]()
, HG
![]()
![]()
∵∠BFH=∠BAC=90°∴BC=![]() =
=![]() ,HG=
,HG=![]() ,∠BFH=∠DHI=90°
,∠BFH=∠DHI=90°
∴cos∠FBH=![]() =
=![]()
∴![]() =
=![]()
∴BF=![]()
∴Rt△BFH中:由勾股定理可得:FH=![]() =
=![]()
∵⊙O的直径为![]() ∴OB=OC=
∴OB=OC=![]() , OF=OB - BF=
, OF=OB - BF=![]() -
-![]() =
=![]()
∵∠OFD=∠BFH=90°
∴DF=![]() =
=![]() ,DH=DF+FH=
,DH=DF+FH=![]() =HG
=HG
∵tan∠HDI=![]() =
=![]() =
=![]() =
=![]() 即HI=
即HI=![]() , IG=HI - HG=
, IG=HI - HG=![]() -
-![]() =
=![]()
∴Rt△DHI中:由勾股定理可得:DI=![]() =
=![]() , OI=DI - OD=
, OI=DI - OD=![]() -
-![]() =
=![]()
∵HG∥AC
∴△OCJ∽△IGJ
∴![]() =
=![]()
∴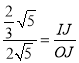 ,
,
∴OJ=3IJ
∴![]()
∴DJ=OD+OJ=![]() +
+![]() =
=![]()
∴DJ的长为![]()


科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.打开电视,它正在播天气预报是不可能事件
B.要考察一个班级中学生的视力情况适合用抽样调查
C.抛掷一枚均匀的硬币,正面朝上的概率是![]() ,若抛掷10次,就一定有5次正面朝上.
,若抛掷10次,就一定有5次正面朝上.
D.甲、乙两人射中环数的方差分别为![]() ,
,![]() ,说明乙的射击成绩比甲稳定
,说明乙的射击成绩比甲稳定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是某款篮球架的示意图,支架AC与底座BC所成的∠ACB=65°,支架AB⊥BC,篮球支架HE∥BC,且篮板DF⊥HE于点E,已知底座BC=1米,AH=![]() 米,HF=
米,HF=![]() 米,HE=1米.
米,HE=1米.
(1)求∠FHE的度数;
(2)已知该款篮球架符合国际篮联规定的篮板下沿D距地面2.90米的规定,求DE的长度.(参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.41,![]() ≈1.41)
≈1.41)

查看答案和解析>>
科目:初中数学 来源: 题型:
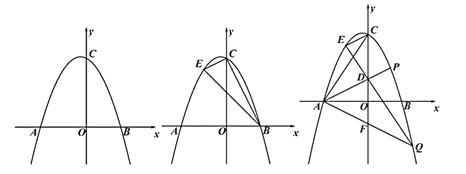
【题目】如图,已知抛物线![]() 交
交![]() 轴于
轴于![]() 两点,交
两点,交![]() 轴正半轴于
轴正半轴于![]() ,且
,且![]() .
.
(1)求![]() 两点的坐标;
两点的坐标;
(2)![]() 是第二象限抛物线上一点,坐标为
是第二象限抛物线上一点,坐标为![]() ,连接
,连接![]() ,求
,求![]() 的面积;
的面积;
(3)在(2)的条件下,![]() 是第一象限抛物线上一点,连接
是第一象限抛物线上一点,连接![]() 交
交![]() 轴于
轴于![]() ,连接
,连接![]() 并延长交抛物线与点
并延长交抛物线与点![]() ,连接
,连接![]() 交
交![]() 轴于
轴于![]() ,将点
,将点![]() 绕点
绕点![]() 逆时针旋转90°得到点
逆时针旋转90°得到点![]() 连接
连接![]() ,若
,若![]() 轴,求Q点坐标.
轴,求Q点坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
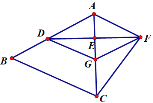
【题目】如图,AB=BC,点D为边AB的中点,点G为AC边的中点,AF∥BC且AD=AF.点E为DF与AC的交点,若AB=6,AE=1,则CF的长为___.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() ,
,![]() ,点
,点![]() 在线段
在线段![]() 上,
上,![]() 是直线
是直线![]() 上一点.
上一点.
(1)如图1,若![]() ,点
,点![]() 在
在![]() 的延长线上,且
的延长线上,且![]() .求证:
.求证:![]() ;
;
(2)如图2,若![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 在线段
在线段![]() 上,点
上,点![]() 是
是![]() 上的一个动点(点
上的一个动点(点![]() 与点
与点![]() ,
,![]() 不重合),矩形
不重合),矩形![]() 的顶点
的顶点![]() ,
,![]() 分别在
分别在![]() ,
,![]() 上.探究
上.探究![]() 与
与![]() 的关系,并给出证明;
的关系,并给出证明;
(3)在(2)的条件下,当点![]() 满足什么条件时,线段
满足什么条件时,线段![]() 的长最短?(直接给出结论,不必说明理由)
的长最短?(直接给出结论,不必说明理由)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,四边形![]() 内接于直径为
内接于直径为![]() 的圆,
的圆,![]() .
.
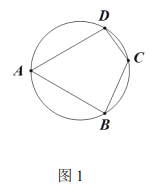
(1)①![]() _ ;
_ ;
②四边形![]() 的周长最大值为_ ;
的周长最大值为_ ;
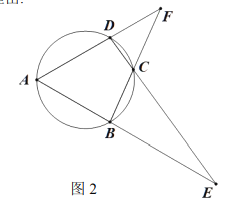
![]() 如图2,延长
如图2,延长![]() 相交于点
相交于点![]() ,延长
,延长![]() 相交于点
相交于点![]() 求
求![]() 与的
与的![]() 积;
积;
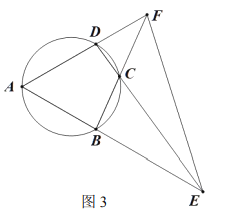
![]() 如图3,连接
如图3,连接![]() 请问在线段
请问在线段![]() 上是否存在点
上是否存在点![]() 与点
与点![]() 关于直线
关于直线![]() 对称,若存在,请证明;若不存在,请说明理由.
对称,若存在,请证明;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,a≠0,c>0)的自变量x与函数值y的部分对应值如表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y=ax2+bx+c | … | p | t | n | t | 0 | … |
有下列结论:①b>0;②关于x的方程ax2+bx+c=0的两个根是0和3;③p+2t<0;④m(am+b)≤﹣4a﹣c(m为任意实数).其中正确结论的个数是( )
A.1B.2C.3D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com