
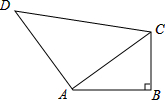
 如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.
如图,∠B=90°,AB=4cm,BC=3cm,AD=12cm,CD=13cm,求四边形ABCD的面积.| AB2+BC2 |
| 32+42 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
| y-3 |
| 2 |
| 2 y+1 |
| 3 |
|
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
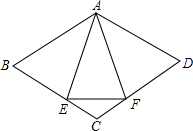 已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,∠BAF=∠DAE.
已知:如图,菱形ABCD中,E、F分别是CB、CD上的点,∠BAF=∠DAE.查看答案和解析>>
科目:初中数学 来源: 题型:
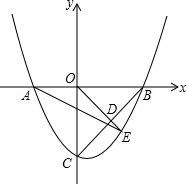 如图,对称轴为直线x=
如图,对称轴为直线x=| 1 |
| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
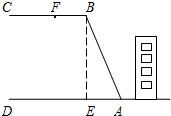 某居民楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为30米,坡角∠BAD=75°.为了减缓坡面防止山体滑坡,居委会决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,坡顶B沿BC向左移15米到F点处,问这样改造能确保安全吗?(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,tan49°30′≈1.17,tan51°57′≈1.28)
某居民楼后面紧邻着一个山坡,坡上面是一块平地,如图所示,BC∥AD,BE⊥AD,斜坡AB长为30米,坡角∠BAD=75°.为了减缓坡面防止山体滑坡,居委会决定对该斜坡进行改造.经地质人员勘测,当坡角不超过50°时,可确保山体不滑坡.如果改造时保持坡脚A不动,坡顶B沿BC向左移15米到F点处,问这样改造能确保安全吗?(参考数据:sin75°≈0.97,cos75°≈0.26,tan75°≈3.73,tan49°30′≈1.17,tan51°57′≈1.28)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com