
【题目】在△ABC中,AB=2![]() ,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
,AC=4,BC=2,以AB为边向△ABC外作△ABD,使△ABD为等腰直角三角形,求线段CD的长.
【答案】2![]() 或2
或2![]() 或3
或3![]()
【解析】
根据题意中的△ABD为等腰直角三角形,显然应分为三种情况:∠ABD=90°,∠BAD=90°,∠ADB=90°.然后巧妙构造辅助线,出现全等三角形和直角三角形,利用全等三角形的性质和勾股定理进行求解.
∵AC=4,BC=2,![]()
∴AC2+BC2=AB2,
∴△ACB为直角三角形,
∠ACB=90°.
分三种情况:如图(1),过点D作DE⊥CB,垂足为点E.
∵DE⊥CB,
∴∠BED=∠ACB=90°,
∴∠CAB+∠CBA=90°.
∵△ABD为等腰直角三角形,
∴AB=BD,∠ABD=90°,
∴∠CBA+∠DBE=90°,
∴∠CAB=∠EBD.
在△ACB与△BED中,
∵∠ACB=∠BED,∠CAB=∠EBD,AB=BD,
∴△ACB≌△BED(AAS),
∴BE=AC=4,DE=CB=2,
∴CE=6.根据勾股定理得![]()
如图(2),过点D作DE⊥CA,垂足为点E.
∵BC⊥CA,∴∠AED=∠ACB=90°,
∴∠EAD+∠EDA=90°.
∵△ABD为等腰直角三角形,∴AB=AD,∠BAD=90°,
∴∠CAB+∠DAE=90°,
∴∠BAC=∠ADE.在△ACB与△DEA中,
∵∠ACB=∠DEA,∠CAB=∠EDA, AB=DA,
∴△ACB≌△DEA(AAS),
∴DE=AC=4,AE=BC=2,
∴CE=6,根据勾股定理得![]()
如图(3),过点D作DE⊥CB,垂足为点E,过点A作AF⊥DE,垂足为点F.∵∠C=90°,
∴∠CAB+∠CBA=90°.
∵∠DAB+∠DBA=90°,
∴∠EBD+∠DAF=90°.
∵∠EBD+∠BDE=90°,∠DAF+∠ADF=90°,
∴∠DBE=∠ADF.
∵∠BED=∠AFD=90°,DB=AD,
∴△AFD≌△DEB,则ED=AF.
由∠ACB=∠CED=∠AFE=90°,则四边形CEFA是矩形,故CE=AF,EF=AC=4.
设DF=x,则BE=x,故EC=2+x,AF=DE=EF-DF=4-x,则2+x=4-x,解得x=1,
故EC=DE=3,
则![]()


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,△ACD中,已知AB⊥CD,且BD>CB,△BCE和△ABD都是等腰直角三角形,王刚同学说有下列全等三角形:
①△ABC≌△DBE;②△ACB≌△ABD;
③△CBE≌△BED;④△ACE≌△ADE.
这些三角形真的全等吗?简要说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
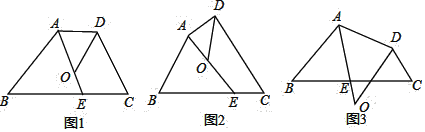
【题目】四边形ABCD中,∠BAD的角平分线与边BC交于点E,∠ADC的角平分线交直线AE于点O.
(1)若点O在四边形ABCD的内部,
①如图1,若AD∥BC,∠B=40°,∠C=70°,则∠DOE= °;
②如图2,试探索∠B、∠C、∠DOE之间的数量关系,并将你的探索过程写下来.
(2)如图3,若点O在四边形ABCD的外部,请你直接写出∠B、∠C、∠DOE之间的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一根24cm的筷子置于底面直径为8cm,高为15cm的圆柱形水杯中,如图所示,设筷子露在杯子外面的长度为hcm,则h的取值范围是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在四边形ABCD中,∠DAB被对角线AC平分,且AC2=ABAD.我们称该四边形为“可分四边形”,∠DAB称为“可分角”.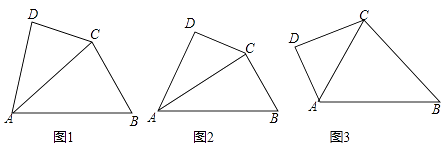
(1)如图2,在四边形ABCD中,∠DAB=60°,AC平分∠DAB,且∠BCD=150°,求证:四边形ABCD为“可分四边形”;
(2)如图3,四边形ABCD为“可分四边形”,∠DAB为“可分角”,如果∠DCB=∠DAB,则求∠DAB的度数;
(3)现有四边形ABCD为“可分四边形”,∠DAB为“可分角”,且AC=4,则△DAB的最大面积等于 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】计算.
(1)﹣7+(﹣8)﹣(﹣18)﹣13
(2)(﹣1)3×(﹣5)﹣(﹣3)÷(﹣![]() )
)
(3)(![]() -
-![]() -
-![]() )÷(﹣
)÷(﹣![]() )
)
(4)﹣12018﹣2![]() ×[13﹣(﹣5)2]
×[13﹣(﹣5)2]
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场11月初花费15 000元购进一批某品牌英语点读笔,因深受顾客喜爱,销售一空.该商场于12月初又花费24 000元购进一批同品牌英语点读笔,且所购数量是11月初的1.5倍,但每支进价涨了10元.
(1)求商场11月初购进英语点读笔多少支?
(2)11月份商场该品牌点读笔每支的售价是270元,若12月份购买的点读笔全部售完,且所获利润是11月份利润的1.2倍,求12月份该品牌点读笔每支的售价?
查看答案和解析>>
科目:初中数学 来源: 题型:
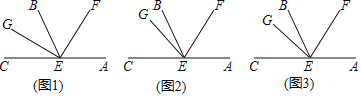
【题目】如图,E是直线AC上一点,EF是∠AEB的平分线.
(1)如图1,若EG是∠BEC的平分线,求∠GEF的度数;
(2)如图2,若GE在∠BEC内,且∠CEG=3∠BEG,∠GEF=75°,求∠BEG的度数.
(3)如图3,若GE在∠BEC内,且∠CEG=n∠BEG,∠GEF=α,求∠BEG(用含n、α的代数式表示).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com