
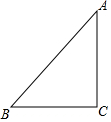
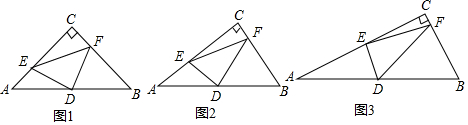
 如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.
如图,已知△ABC中,∠C=90°,AC=BC=$\sqrt{2}$,将△ABC绕点A顺时针方向旋转60°到△AB′C′的位置,连接C′B.分析 (1)根据题意作出图形即可;
(2)连接BB′,延长BC′交AB′于点M;根据全等三角形的性质得到得到∠MBB′=∠MBA=30°;求出BM、C′M的长,即可解决问题.
解答 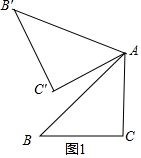 解:(1)如图1所示,
解:(1)如图1所示,
(2)如图2,连接BB′,延长BC′交AB′于点M;
由题意得:∠BAB′=60°,BA=B′A,
∴△ABB′为等边三角形,
∴∠ABB′=60°,AB=B′B;
在△ABC′与△B′BC′中,
$\left\{\begin{array}{l}{AC′=B′C′}\\{AB=B′B}\\{BC′=BC′}\end{array}\right.$,
∴△ABC′≌△B′BC′(SSS),
∴∠MBB′=∠MBA=30°,
∴BM⊥AB′,且AM=B′M;
由题意得:AB2=16,
∴AB′=AB=4,AM=2,
∴C′M=$\frac{1}{2}$AB′=2;由勾股定理可求:BM=2$\sqrt{3}$,
∴C′B=2$\sqrt{3}$-2.
点评 本题考查了旋转的性质,全等三角形的判定与性质,等边三角形的判定与性质,等腰直角三角形的性质,作辅助线构造出全等三角形并求出BC′在等边三角形的高上是解题的关键,也是本题的难点.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
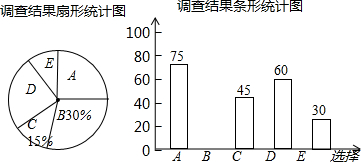
| 造成医患关系紧张的原因(单选) A.药价高 B.检测项目太多且收费太高 C.住院报销比例低 D.医疗费与个人收入不相称 E.其他 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.
某校1200名学生参加了全市组织的“经典诵读”活动,该校随机选取部分学生,对他们在三、四两个月的诵读时间进行调查,下面是根据调查数据制作的统计图表的一部分,三月日人均诵读时间的频数分布直方图.| 日人均诵读时间x/h | 人数 | 百分比 |
| 0≤x≤0.5 | 6 | |
| 0.5<x≤1 | 30 | |
| 1<x≤1.5 | 50% | |
| 1.5<x≤2 | 10 | 10% |
| 2<x≤2.5 | b | c |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
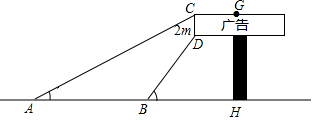 数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长($\sqrt{3}≈1.73$,要求结果精确得到0.1m)
数学兴趣小组想利用所学的知识了解某广告牌的高度(图中GH的长),经测量知CD=2m,在B处测得点D的仰角为60°,在A处测得点C的仰角为30°,AB=10m,且A、B、H三点共线,请根据以上数据计算GH的长($\sqrt{3}≈1.73$,要求结果精确得到0.1m)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com