
����Ŀ������һ�������Σ����������ڽǵĶ����ֱ�Ϊx�㡢y���z�㣬��x��y��z����x2+y2��z2�����Ƕ������������Ϊ���������Σ�
��1����ABC�У�����A��40�㣬��B��80�㣬���ABC�� ������ǡ����ǡ������������Σ�
��2����ͼ����ǡ�ABC�ǡ�O���ڽ������Σ���C��60�㣬AC��2����O��ֱ����2![]() ����֤����ABC�����������Σ�
����֤����ABC�����������Σ�
��3����֪��ABC�����������Σ���A��30�㣬���C�Ķ�����
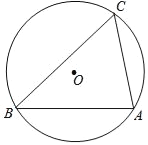
���𰸡���1�����ǣ���2������������3����C��78���72��.
��������
��1���������������εĶ���ó���ABC����״����������ɣ�
��2�����ù��ɶ������涨���ó���ABC����״�����ó��𰸣�
��3���������������εĶ�������ֱ�ó���C�Ķ�����
��1���ߡ�ABC�У���A��40������B��80����
���C��60��
��402+602��802��
���ABC��������������
�ʴ�Ϊ�����ǣ�
��2��֤��������OA��OC��
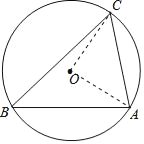
��AC��2��OA��OC��![]() ��
��
���OAC��ֱ�������Σ�����AOC��90����
���B��45����
�ߡ�C��60����
���A��75����
�������ڽ������ϵ��452+602��5625��752��
���ABC������������
��3�����C��x�������B����150��x������
����CΪ���ǣ���x2����150��x��2+302��
���x��78��
����B���ǣ���150��x��2��x2+302��
���x��72��
���Ͽ�֪����C��78����72��


 ��У���һ��ͨϵ�д�
��У���һ��ͨϵ�д� �γ̴����Ծ�����100��ϵ�д�
�γ̴����Ծ�����100��ϵ�д� �¾�����ĩ���100��ϵ�д�
�¾�����ĩ���100��ϵ�д� ȫ�ܴ���100��ϵ�д�
ȫ�ܴ���100��ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����С���ͬѧ�������ʵ����е�����20����ͥ���µ��õ����������ʾ:
�õ���(ǧ��ʱ) | 120 | 140 | 160 | 180 | 200 |
���� | 2 | 3 | 6 | 7 | 2 |
����20����ͥ�����õ�������������λ����ƽ�����ֱ���( )
A. 180��160��164B. 160��180��164
C. 160��160��164D. 180��180��164
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�AD�Ǹߣ�����PQMN�Ķ���P��N�ֱ���AB��AC�ϣ�QM�ڱ�BC�ϣ���BC��8cm��AD��6cm����PN��2PQ�������PQMN���ܳ�Ϊ��������
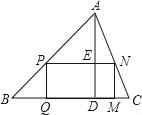
A. 14.4cmB. 7.2cmC. 11.52cmD. 12.4cm
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
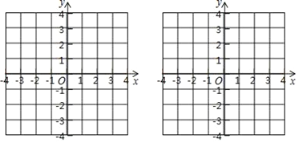
����Ŀ����ͼ���ڽ�����ƽ��ֱ������ϵ�������������У�A��2��2����B��1��0����C��3��1��
��1��������ABC����x��ԳƵ���A1B1C1��
��2����������ABC�Ƶ�B��ʱ����ת90�������õ���A2B2C2����ֱ��д��A2������꣮
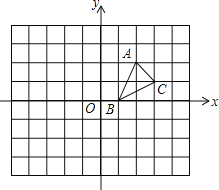
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
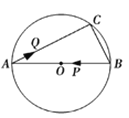
����Ŀ����ͼ��AB�ǡ�O��ֱ������BC=6cm��AC=8cm��������P��2cm/s���ٶȴ�B���������B��A�ķ����˶�����Q��1cm/s���ٶȴ�A���������A��C�ķ����˶�������P�����Aʱ����QҲ��ֹ֮ͣ�˶������˶�ʱ��Ϊt(s)������APQ��ֱ��������ʱ��t��ֵΪ___________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ijһ�����������¶��壺������ʵ��m���Ա�����ֵΪm ʱ������ֵ����m�����mΪ��������ķ���ֵ.�ں������ڷ���ֵʱ���ú����������ֵ����С����ֵ֮��n��Ϊ��������ķ������.�ر�أ�������ֻ��һ������ֵʱ���䷴�����nΪ��. ���磺ͼ�еĺ����� 4����1��������ֵ���䷴����� n ���� 5. ���к���y��![]() ������������ķ����������п���ֵ�У� ��
������������ķ����������п���ֵ�У� ��
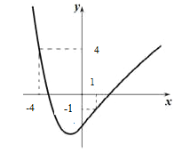
A. 1��B. 2��C. 3�������ϵ�����D. ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵxOy�У��С�������ϵ��y������x��m��2+4m��3������Ϊ��P����Щ�����ߵ���״�������� y����x2 ��ͬ��������λ�ò�ͬ��
��1����д�±�����˵������mȡ��ͬ��ֵʱ����Pλ�õı仯����ʲô������
m��ֵ | �� | ��1 | 0 | 1 | 2 | �� |
��P���� | �� | �� |
��2���������ߵĶԳ�����ֱ��x��1�����ȷ��m��ֵ����M��p��q��Ϊ���������ϵ�һ�����㣬�ҩ�1��p��2����ֱ��y��kx��4��k��0��ʼ�վ�����M��
�������������x��Ľ������ꣻ
����k��ȡֵ��Χ��
��3������Q��x���ϣ���S��0����1����y���ϣ���R������ƽ���ڣ����Ե�P��Q��R��SΪ������ı����������Σ���ֱ��д�����е�Q�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
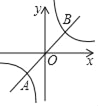
����Ŀ������y��x��ͼ���뺯��y��![]() ��ͼ���ڵ�һ�����ڽ��ڵ�A��B(2��m)���㣮
��ͼ���ڵ�һ�����ڽ��ڵ�A��B(2��m)���㣮
(1)���������y��![]() �Ľ���ʽ��
�Ľ���ʽ��
(2)�����ͼ���жϵ�һ�κ�����ֵ���ڷ�����������ֵʱx��ȡֵ��Χ��
(3)��C�Ǻ���y��![]() �ڵ�һ����ͼ���ϵ�һ�����㣬��OBC�����Ϊ3ʱ���������C�����꣮
�ڵ�һ����ͼ���ϵ�һ�����㣬��OBC�����Ϊ3ʱ���������C�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵȱ�![]() �У�
�У�![]() ����D���߶�BC�ϵ�һ���㣬����AD������D��
����D���߶�BC�ϵ�һ���㣬����AD������D��![]() ������ΪD��������AC���
������ΪD��������AC���![]() ��BDΪxcm��CEΪycm��
��BDΪxcm��CEΪycm��
С�ϸ���ѧϰ�����ľ��飬�Ժ���y���Ա���x�ı仯���仯�Ĺ��ɽ�����̽����
������С�ϵ�̽�����̣��벹��������
![]() ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
ͨ��ȡ�㡢��ͼ���������õ���x��y�ļ���ֵ�����±���
| 0 |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
|
|
|
| ___ |
| 0 |
|
|
|
| 0 |
![]() ˵������ȫ�����������ֵ����һλС��
˵������ȫ�����������ֵ����һλС��![]()
![]() ����ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
����ƽ��ֱ������ϵ������Բ�ȫ��ı��и��Զ�ӦֵΪ����ĵ㣬�����ú�����ͼ��
![]() ��ϻ����ĺ���ͼ������⣺���߶�BD���߶�CE����2��ʱ��BD�ij���ԼΪ_____cm��
��ϻ����ĺ���ͼ������⣺���߶�BD���߶�CE����2��ʱ��BD�ij���ԼΪ_____cm��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com