
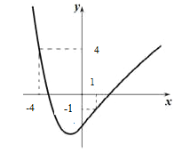
【题目】对于某一函数给出如下定义:若存在实数m,自变量的值为m 时,函数值等于m,则称m为这个函数的反向值.在函数存在反向值时,该函数的最大反向值与最小反向值之差n称为这个函数的反向距离.特别地,当函数只有一个反向值时,其反向距离n为零. 例如:图中的函数有 4,-1两个反向值,其反向距离 n 等于 5. 现有函数y=![]() ,则这个函数的反向距离的所有可能值有( )
,则这个函数的反向距离的所有可能值有( )
A. 1个B. 2个C. 3个及以上的有限个D. 无数个
科目:初中数学 来源: 题型:
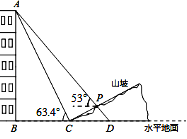
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(问题情境)如图,Rt△ABC中,∠ACB=90°,CD⊥AB,我们可以利用△ABC与△ACD相似证明AC2=AD·AB,这个结论我们称之为射影定理,试证明这个定理;
(结论运用)如图,正方形ABCD的边长为6,点O是对角线AC、BD的交点,点E在CD上,过点C作CF⊥BE,垂足为F,连接OF.
(1)试利用射影定理证明△ABC∽△BED;
(2)若DE=2CE,求OF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6cm的⊙O中,点A是劣弧BC的中点,点D是优弧BC上一点,且∠D=30°,下列四个结论:①OA⊥BC;②BC=6![]() cm;③sin∠AOB=
cm;③sin∠AOB=![]() ;④四边形ABOC是菱形.其中正确结论的序号是( )
;④四边形ABOC是菱形.其中正确结论的序号是( )
A. ①③ B. ①②③④ C. ②③④ D. ①③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.
(1)△ABC中,若∠A=40°,∠B=80°,则△ABC (填“是”或“不是”)美好三角形;
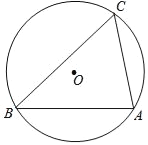
(2)如图,锐角△ABC是⊙O的内接三角形,∠C=60°,AC=2,⊙O的直径是2![]() ,求证:△ABC是美好三角形;
,求证:△ABC是美好三角形;
(3)已知△ABC是美好三角形,∠A=30°,求∠C的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市某公司分两次采购了一批原料,已知第二次的采购数量是第一次采购数量的两倍,其它信息如下表:
第一次 | 第二次 | |
每吨原料的价格(元) | m+500 | m-500 |
采购费用(万元) | 40 | 60 |
(1)求m的值,并求出这两次共采购了多少吨原料?
(2)该公司可将原料加工成A型产品或B型产品,而受设备限制每天只能安排加工一种型号产品.经统计,加工A型产品与B型产品各1天共需用原料数为20吨,加工3天A型产品与加工2天B型产品所需用原料数相等.请求出加工成A,B型产品每天所需的原料数分别是多少吨?
(3)该公司将生产的两种产品全部出口国外,每吨原料加工成A,B型产品后的获利分别是1000元与600元,但要求加工时间不超过30天.为了使总利润获得最大,应采用怎样的加工方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
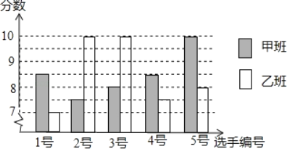
【题目】中国经济的快速发展让众多国家感受到了威胁,随着钓鱼岛事件、南海危机、萨德入韩等系列事件的发生,国家安全一再受到威胁,所谓“国家兴亡,匹夫有责”,某校积极开展国防知识教育,九年级甲、乙两班分别选5名同学参加“国防知识”比赛,其预赛成绩如图所示:
(1)根据如图填写如表:
平均数 | 中位数 | 众数 | 方差 | |
甲班 | 8.5 | 8.5 | ||
乙班 | 8.5 | 10 | 1.6 |
(2)根据如表数据,分析哪个班的成绩较好,请详细说明.
查看答案和解析>>
科目:初中数学 来源: 题型:
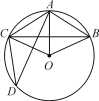
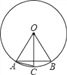
【题目】如图,在⊙O中,OA=AB,OC⊥AB,则下列结论错误的是( )
A. 弦AB的长等于圆内接正六边形的边长
B. 弦AC的长等于圆内接正十二边形的边长
C. ![]()
D. ∠BAC=30°
查看答案和解析>>
科目:初中数学 来源: 题型:
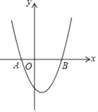
【题目】如图,在平面直角坐标系中抛物线y=(x+1)(x﹣3)与x轴相交于A、B两点,若在抛物线上有且只有三个不同的点C1、C2、C3,使得△ABC1、△ABC2、△ABC3的面积都等于m,则m的值是( )
A. 6 B. 8 C. 12 D. 16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com