练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

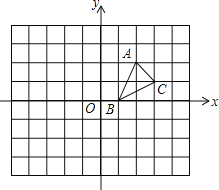
    【题目】如图，在建立了平面直角坐标系的正方形网格中，A（2，2），B（1，0），C（3，1）

    （1）画出△ABC关于x轴对称的△A1B1C1．

    （2）画出将△ABC绕点B逆时针旋转90°，所得的△A2B2C2．并直接写出A2点的坐标．

    【答案】（1）△A1B1C1如图所示；见解析； （2）△A2B2C2如图所示；见解析； 点A2的坐标为（﹣1，1）．

    【解析】

    （1）根据网格结构找出点A、B、C关于x轴的对称点A1、B1、C1的位置，然后顺次连接即可；
    （2）根据网格结构找出点A、B、C绕点B逆时针旋转90°的对应点A2、B2、C2的位置，然后顺次连接即可；

    （1）△A1B1C1如图所示；

    （2）△A2B2C2如图所示；

    点A2的坐标为（﹣1，1）．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

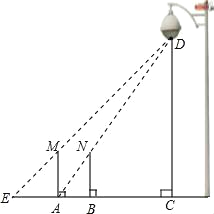
    【题目】一天晚上，李明利用灯光下的影子长来测量一路灯D的高度．如图，当在点A处放置标杆时，李明测得直立的标杆高AM与影子长AE正好相等，接着李明沿AC方向继续向前走，走到点B处放置同一个标杆，测得直立标杆高BN的影子恰好是线段AB，并测得AB＝1.2m，已知标杆直立时的高为1.8m，求路灯的高CD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

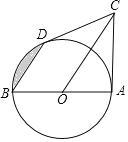
    【题目】如图，AB是⊙O的直径，CD切⊙O于点D，且BD∥OC，连接AC．
    （1）求证：AC是⊙O的切线；
    （2）若AB=OC=4，求图中阴影部分的面积（结果保留根号和π）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】（问题情境）如图，Rt△ABC中，∠ACB=90°，CD⊥AB，我们可以利用△ABC与△ACD相似证明AC2=AD·AB，这个结论我们称之为射影定理，试证明这个定理；

    （结论运用）如图，正方形ABCD的边长为6，点O是对角线AC、BD的交点，点E在CD上，过点C作CF⊥BE，垂足为F，连接OF．

    （1）试利用射影定理证明△ABC∽△BED；

    （2）若DE=2CE，求OF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某公司从2009年开始投入技术改造资金，经技术改进后，其产品的生产成本不断降低，具体数据如表：

    年度

    2009

    2010

    2011

    2012

    投入技改资金x（万元）

    2.5

    3

    4

    4.5

    产品成本y（万元/件）

    7.2

    6

    4.5

    4

    （1）试判断：从上表中的数据看出，y与x符合你学过的哪个函数模型？请说明理由，并写出它的解析式．

    （2）按照上述函数模型，若2013年已投入技改资金5万元

    ①预计生产成本每件比2012年降低多少元？

    ②如果打算在2013年把每件产品的成本降低到3.2万元，则还需投入技改资金多少万元？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在半径为6cm的⊙O中，点A是劣弧BC的中点，点D是优弧BC上一点，且∠D＝30°，下列四个结论：①OA⊥BC；②BC＝6cm；③sin∠AOB＝；④四边形ABOC是菱形．其中正确结论的序号是（ ）

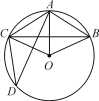
    A. ①③ B. ①②③④ C. ②③④ D. ①③④

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】对于一个三角形，设其三个内角的度数分别为x°、y°和z°，若x、y、z满足x2+y2＝z2，我们定义这个三角形为美好三角形．

    （1）△ABC中，若∠A＝40°，∠B＝80°，则△ABC　 　（填“是”或“不是”）美好三角形；

    （2）如图，锐角△ABC是⊙O的内接三角形，∠C＝60°，AC＝2，⊙O的直径是2，求证：△ABC是美好三角形；

    （3）已知△ABC是美好三角形，∠A＝30°，求∠C的度数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

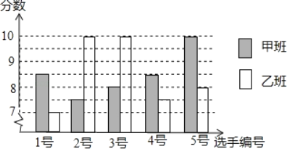
    【题目】中国经济的快速发展让众多国家感受到了威胁，随着钓鱼岛事件、南海危机、萨德入韩等系列事件的发生，国家安全一再受到威胁，所谓“国家兴亡，匹夫有责”，某校积极开展国防知识教育，九年级甲、乙两班分别选5名同学参加“国防知识”比赛，其预赛成绩如图所示：

    （1）根据如图填写如表：

    平均数

    中位数

    众数

    方差

    甲班

    8.5

    8.5

    乙班

    8.5

    10

    1.6

    （2）根据如表数据，分析哪个班的成绩较好，请详细说明．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某村计划建造如图所示的矩形蔬菜温室，要求长与宽的比为2：1．在温室内，沿前侧内墙保留3m宽的空地，其它三侧内墙各保留1m宽的通道．当矩形温室的长与宽各为多少时，蔬菜种植区域的面积是288m2？

    查看答案和解析>>

    同步练习册答案