
ЁОЬтФПЁПФГЙЋЫОДг2009ФъПЊЪМЭЖШыММЪѕИФдьзЪН№ЃЌОММЪѕИФНјКѓЃЌЦфВњЦЗЕФЩњВњГЩБОВЛЖЯНЕЕЭЃЌОпЬхЪ§ОнШчБэЃК
ФъЖШ | 2009 | 2010 | 2011 | 2012 |
ЭЖШыММИФзЪН№xЃЈЭђдЊЃЉ | 2.5 | 3 | 4 | 4.5 |
ВњЦЗГЩБОyЃЈЭђдЊ/МўЃЉ | 7.2 | 6 | 4.5 | 4 |
ЃЈ1ЃЉЪдХаЖЯЃКДгЩЯБэжаЕФЪ§ОнПДГіЃЌyгыxЗћКЯФубЇЙ§ЕФФФИіКЏЪ§ФЃаЭЃПЧыЫЕУїРэгЩЃЌВЂаДГіЫќЕФНтЮіЪНЃЎ
ЃЈ2ЃЉАДееЩЯЪіКЏЪ§ФЃаЭЃЌШє2013ФъвбЭЖШыММИФзЪН№5ЭђдЊ
ЂйдЄМЦЩњВњГЩБОУПМўБШ2012ФъНЕЕЭЖрЩйдЊЃП
ЂкШчЙћДђЫудк2013ФъАбУПМўВњЦЗЕФГЩБОНЕЕЭЕН3.2ЭђдЊЃЌдђЛЙашЭЖШыММИФзЪН№ЖрЩйЭђдЊЃП
ЁОД№АИЁПЃЈ1ЃЉЗДБШР§КЏЪ§ЙиЯЕy=![]()
ЃЈ2ЃЉЂйНЕЕЭ0.4ЭђдЊ Ђк0.63ЭђдЊ
ЁОНтЮіЁП
ЪдЬтЃЈ1ЃЉИљОнЪЕМЪЬтвтКЭЪ§ОнЬиЕуЗжЧщПіЧѓНтЃЌИљОнХХГ§ЗЈПЩжЊЦфЮЊЗДБШР§КЏЪ§ЃЌРћгУД§ЖЈЯЕЪ§ЗЈЧѓНтМДПЩЃЛ
ЃЈ2ЃЉжБНгАбx=5ЭђдЊКЭy=3.2ЗжБ№ДњШыКЏЪ§НтЮіЪНМДПЩЧѓНтЃЎ
НтЃКЃЈ1ЃЉгЩБэжаЪ§ОнжЊЃЌxЁЂyЙиЯЕЃК
xy=2.5ЁС7.5=3ЁС6=4ЁС4.5=4.5ЁС4=18
Ёрxy=18
ЁрxЁЂyВЛЪЧвЛДЮКЏЪ§ЙиЯЕ
ЁрБэжаЪ§ОнЪЧЗДБШР§КЏЪ§ЙиЯЕy=![]() ЃЛ
ЃЛ
ЃЈ2ЃЉЂйЕБx=5ЭђдЊЪБЃЌy=3.6ЃЎ
4Љ3.6=0.4ЃЈЭђдЊЃЉЃЌ
ЁрЩњВњГЩБОУПМўБШ2009ФъНЕЕЭ0.4ЭђдЊЃЎ
ЂкЕБy=3.2ЭђдЊЪБЃЌ3.2=![]() ЃЎ
ЃЎ
Ёрx=5.625ЃЈ1ЗжЃЉ
Ёр5.625Љ5=0.625Ёж0.63ЃЈЭђдЊЃЉ
ЁрЛЙдМашЭЖШы0.63ЭђдЊЃЎ


 ВНВНИпДяБъОэЯЕСаД№АИ
ВНВНИпДяБъОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
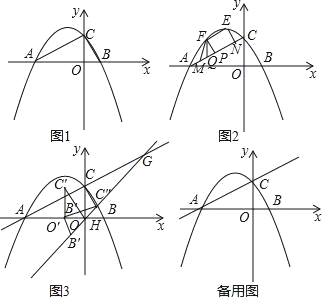
ЁОЬтФПЁПШчЭМ1ЃЌХзЮяЯпyЃНЉ![]() гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгACЁЂBCЃЎ
гыxжсНЛгкAЁЂBСНЕуЃЌгыyжсНЛгкЕуCЃЌСЌНгACЁЂBCЃЎ
ЃЈ1ЃЉЧѓЯпЖЮACЕФГЄЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌEЮЊХзЮяЯпЕФЖЅЕуЃЌFЮЊACЩЯЗНЕФХзЮяЯпЩЯвЛЖЏЕуЃЌMЁЂNЮЊжБЯпACЩЯЕФСНЖЏЕуЃЈMдкNЕФзѓВрЃЉЃЌЧвMNЃН4ЃЌзїFPЁЭACгкЕуPЃЌFQЁЮyжсНЛACгкЕуQЃЎЕБЁїFPQЕФУцЛ§зюДѓЪБЃЌСЌНгEFЁЂENЁЂFMЃЌЧѓЫФБпаЮENMFжмГЄЕФзюаЁжЕЃЎ
ЃЈ3ЃЉШчЭМ3ЃЌНЋЁїBCOбиxжсИКЗНЯђЦНвЦ![]() ИіЕЅЮЛКѓЕУЁїB'C'O'ЃЌдйНЋЁїB'C'O'ШЦЕуO'ЫГЪБеыа§зЊІСЖШЃЌЕУЕНЁїBЁхCЁхO'ЃЈЦфжа0ЁуЃМІСЃМ180ЁуЃЉЃЌа§зЊЙ§ГЬжажБЯпBЁхCЁхгыжБЯпACНЛгкЕуGЃЌгыxжсНЛгкЕуHЃЌЕБЁїAGHЪЧЕШбќШ§НЧаЮЪБЃЌЧѓІСЕФЖШЪ§ЃЎ
ИіЕЅЮЛКѓЕУЁїB'C'O'ЃЌдйНЋЁїB'C'O'ШЦЕуO'ЫГЪБеыа§зЊІСЖШЃЌЕУЕНЁїBЁхCЁхO'ЃЈЦфжа0ЁуЃМІСЃМ180ЁуЃЉЃЌа§зЊЙ§ГЬжажБЯпBЁхCЁхгыжБЯпACНЛгкЕуGЃЌгыxжсНЛгкЕуHЃЌЕБЁїAGHЪЧЕШбќШ§НЧаЮЪБЃЌЧѓІСЕФЖШЪ§ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕБ-2ЁмxЁм1ЪБЃЌЖўДЮКЏЪ§y=-ЃЈx-mЃЉ2+m2+1газюДѓжЕ3ЃЌдђЪЕЪ§mЕФжЕЮЊЃЈЁЁЁЁЃЉ
A. 2Лђ-![]() B.
B. ![]() Лђ-
Лђ-![]() C.
C. ![]() Лђ-
Лђ-![]() D.
D. ![]() Лђ-
Лђ-![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌADЪЧИпЃЌОиаЮPQMNЕФЖЅЕуPЁЂNЗжБ№дкABЁЂACЩЯЃЌQMдкБпBCЩЯЃЌШєBCЃН8cmЃЌADЃН6cmЃЌЧвPNЃН2PQЃЌдђОиаЮPQMNЕФжмГЄЮЊЃЈЁЁЁЁЃЉ
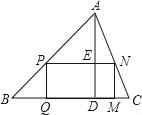
A. 14.4cmB. 7.2cmC. 11.52cmD. 12.4cm
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЦНааЫФБпаЮABCDжаЃЌЙ§ЕуBЕФжБЯпгыЖдНЧЯпACЁЂБпADЗжБ№НЛгкЕуEКЭFЃЎЙ§ЕуEзїEGЁЮBCЃЌНЛABгкGЃЌдђЭМжаЯрЫЦШ§НЧаЮгаЃЈ ЃЉ

A. 4ЖдB. 5ЖдC. 6ЖдD. 7Жд
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдкНЈСЂСЫЦНУцжБНЧзјБъЯЕЕФе§ЗНаЮЭјИёжаЃЌAЃЈ2ЃЌ2ЃЉЃЌBЃЈ1ЃЌ0ЃЉЃЌCЃЈ3ЃЌ1ЃЉ
ЃЈ1ЃЉЛГіЁїABCЙигкxжсЖдГЦЕФЁїA1B1C1ЃЎ
ЃЈ2ЃЉЛГіНЋЁїABCШЦЕуBФцЪБеыа§зЊ90ЁуЃЌЫљЕУЕФЁїA2B2C2ЃЎВЂжБНгаДГіA2ЕуЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌABЪЧЁбOЕФжБОЖЃЌЯвBC=6cmЃЌAC=8cmЃЎШєЖЏЕуPвд2cm/sЕФЫйЖШДгBЕуГіЗЂбизХBЁњAЕФЗНЯђдЫЖЏЃЌЕуQвд1cm/sЕФЫйЖШДгAЕуГіЗЂбизХAЁњCЕФЗНЯђдЫЖЏЃЌЕБЕуPЕНДяЕуAЪБЃЌЕуQвВЫцжЎЭЃжЙдЫЖЏЃЎЩшдЫЖЏЪБМфЮЊt(s)ЃЌЕБЁїAPQЪЧжБНЧШ§НЧаЮЪБЃЌtЕФжЕЮЊ___________ЃЎ
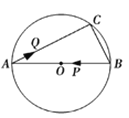
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЦНУцжБНЧзјБъЯЕxOyжаЃЌгаЁАХзЮяЯпЯЕЁБyЃНЃЃЈxЃmЃЉ2+4mЃ3ЃЌЖЅЕуЮЊЕуPЃЌетаЉХзЮяЯпЕФаЮзДгыХзЮяЯп yЃНЃx2 ЯрЭЌЃЌЕЋЖЅЕуЮЛжУВЛЭЌЃЎ
ЃЈ1ЃЉЬюаДЯТБэЃЌВЂЫЕГіЃКдкmШЁВЛЭЌЪ§жЕЪБЃЌЕуPЮЛжУЕФБфЛЏОпгаЪВУДЬиеїЃП
mЕФжЕ | Ё | Ѓ1 | 0 | 1 | 2 | Ё |
ЕуPзјБъ | Ё | Ё |
ЃЈ2ЃЉШєХзЮяЯпЕФЖдГЦжсЪЧжБЯпxЃН1ЃЌдђПЩШЗЖЈmЕФжЕЃЎЕуMЃЈpЃЌqЃЉЮЊДЫХзЮяЯпЩЯЕФвЛИіЖЏЕуЃЌЧвЉ1ЃМpЃМ2ЃЌЖјжБЯпyЃНkxЃ4ЃЈkЁй0ЃЉЪМжеОЙ§ЕуMЃЎ
ЂйЧѓДЫХзЮяЯпгыxжсЕФНЛЕузјБъЃЛ
ЂкЧѓkЕФШЁжЕЗЖЮЇЃЎ
ЃЈ3ЃЉШєЕуQдкxжсЩЯЃЌЕуSЃЈ0ЃЌЃ1ЃЉдкyжсЩЯЃЌЕуRдкзјБъЦНУцФкЃЌЧввдЕуPЃЌQЃЌRЃЌSЮЊЖЅЕуЕФЫФБпаЮЪЧе§ЗНаЮЃЌЪджБНгаДГіЫљгаЕуQЕФзјБъЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌдке§ЗНаЮABCDжаЃЌEЁЂFЪЧЖдНЧЯпBDЩЯСНЕуЃЌЧвЁЯEAF=45ЁуЃЌНЋЁїADFШЦЕуAЫГЪБеыа§зЊ90ЁуКѓЃЌЕУЕНЁїABQЃЌСЌНгEQЃЌЧѓжЄЃК
ЃЈ1ЃЉEAЪЧЁЯQEDЕФЦНЗжЯпЃЛ
ЃЈ2ЃЉEF2=BE2+DF2ЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com