
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )

A. 4对B. 5对C. 6对D. 7对
【答案】B
【解析】
试题根据平行四边形的性质得出AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,推出△ABC≌△CDA,即可推出△ABC∽△CDA,根据相似三角形的判定定理:平行于三角形一边的直线截其它两边或其它两边的延长线,所截的三角形与原三角形相似即可推出其它各对三角形相似.
解:图中相似三角形有△ABC∽△CDA,△AGE∽△ABC,△AFE∽△CBE,△BGE∽△BAF,△AGE∽△CDA共5对,
理由是:∵四边形ABCD是平行四边形,
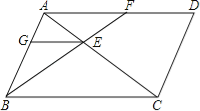
∴AD∥BC,AB∥CD,AD=BC,AB=CD,∠D=∠ABC,
∴△ABC≌△CDA,即△ABC∽△CDA,
∵GE∥BC,
∴△AGE∽△ABC∞△CDA,
∵GE∥BC,AD∥BC,
∴GE∥AD,
∴△BGE∽△BAF,
∵AD∥BC,
∴△AFE∽△CBE.
故选B.


科目:初中数学 来源: 题型:
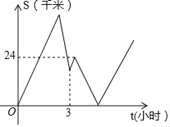
【题目】自行车远动员甲准备参加一项国际自行车赛事,为此特地骑自行车从A地出发,匀速前往168千米外的B地进行拉练.出发2小时后,乙发现他忘了带某训练用品,于是马上骑摩托车从A地出发匀速去追甲送该用品.已知乙骑摩托车的速度比甲骑自行车的速度每小时多30千米,但摩托车行驶一小时后突遇故障,修理15分钟后,又上路追甲,但速度减小了![]() ,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
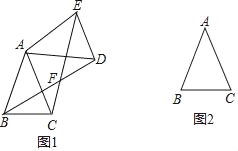
【题目】在△ABC中,AB=AC=2,∠BAC=45°.将△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,B,C两点的对应点分别为点D,E,BD,CE所在直线交于点F.
(1)当△ABC旋转到图1位置时,∠CAD= (用α的代数式表示),∠BFC的度数为 °;
(2)当α=45时,在图2中画出△ADE,并求此时点A到直线BE的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是否为等腰三角形,并说明理由.
(2)若AB=1,∠ABE=45°,求BC的长.
(3)在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE是什么特殊平行四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
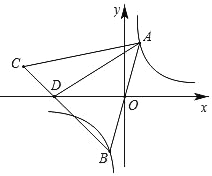
【题目】如图,已知点A是反比例函数y=![]() 的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为__.
的图象在第一象限上的动点,连结AO并延长交另一分支于点B,以AB为边作等边△ABC使点C落在第二象限,且边BC交x轴于点D,若△ACD与△ABD的面积之比为1:2,则点C的坐标为__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
年度 | 2009 | 2010 | 2011 | 2012 |
投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
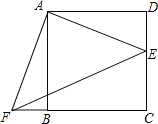
【题目】如图,点E是正方形ABCD的边DC上一点,把△ADE顺时针旋转△ABF的位置.
(1)旋转中心是点 ,旋转角度是 度;
(2)若连结EF,则△AEF是 三角形;并证明;
(3)若四边形AECF的面积为25,DE=2,求AE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
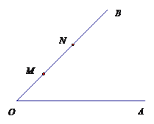
【题目】如图,∠AOB=45°,点M,N在边OB上,OM=x,ON=x+4,点P是边OA上的点,且△PMN是等腰三角形.在x>2的条件下,(1)当x=______时,符合条件的点P只有一个;(2)当x=______时,符合条件的点P恰好有三个.(两个小题都只写出一个数即可)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com