
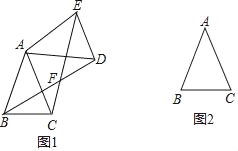
【题目】在△ABC中,AB=AC=2,∠BAC=45°.将△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,B,C两点的对应点分别为点D,E,BD,CE所在直线交于点F.
(1)当△ABC旋转到图1位置时,∠CAD= (用α的代数式表示),∠BFC的度数为 °;
(2)当α=45时,在图2中画出△ADE,并求此时点A到直线BE的距离.
【答案】(1)α﹣45°,45°;(2)图详见解析,点A到直线BE的距离为![]() .
.
【解析】
(1)如图1,利用旋转的性质得∠BAD=∠CAE=α,AB=AD,AE=AC,则∠CAD=α﹣45°;再利用等腰三角形的性质和三角形内角和得到∠ABD=∠ACE,所以∠BFC=∠BAC=45°.
(2)如图2,△ADE为所作,BE与AC相交于G,利用旋转的性质得点D与点C重合,∠CAE=45°,AE=AB=2,则△ABE为等腰直角三角形,所以BE=![]() AB=2
AB=2![]() ,再证明AG⊥BE,然后根据等腰直角三角形的性质求出AG的长即可.
,再证明AG⊥BE,然后根据等腰直角三角形的性质求出AG的长即可.
解:(1)∵△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,如图1,
∴∠BAD=∠CAE=α,AB=AD,AE=AC,
而∠BAC=45°,
∴∠CAD=α﹣45°;
∵AB=AD,AE=AC,
∴∠ABD=∠ADB=![]() (180°﹣∠BAD)=
(180°﹣∠BAD)=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,∠ACE=∠AEC=
α,∠ACE=∠AEC=![]() (180°﹣α)=90°﹣
(180°﹣α)=90°﹣![]() α,
α,
∴∠ABD=∠ACE,
∴∠BFC=∠BAC=45°.
故答案为α﹣45°;45°;

(2)如图2,△ADE为所作,BE与AC相交于G,
∵△ABC绕点A逆时针旋转45度得到△ADE,
而AB=AC,∠BAC=45°,
∴点D与点C重合,∠CAE=45°,AE=AB=2,
∴△ABE为等腰直角三角形,
∴BE=![]() AB=2
AB=2![]() ,
,
而AG平分∠BAE,
∴AG⊥BE,
∴AG=![]() BE=
BE=![]() ,
,
即此时点A到直线BE的距离为![]() .
.


 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:初中数学 来源: 题型:
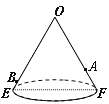
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为6 cm,母线OE(OF)长为9cm.在母线OF上的点A处有一块爆米花残渣,且FA = 3cm.在母线OE上的点B处有一只蚂蚁,且EB = 1cm.这只蚂蚁从点B处沿圆锥表面爬行到A点,则爬行的最短距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
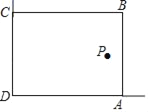
【题目】在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用32m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm.
(1)若花园的面积为252m2,求x的值;
(2)若在P处有一棵树与墙CD,AD的距离分别是17m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积S的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,与x轴的一个交点A在点(﹣3,0)和(﹣2,0)之间,其部分图象如图,则下列结论:①4ac﹣b2<0;②2a﹣b=0;③a+b+c<0;④点M(x1,y1)、N(x2,y2)在抛物线上,若x1<x2<﹣1,则y1>y2,⑤abc>0.其中正确结论的个数是( )

A. 5个 B. 4个 C. 3个 D. 2个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,AB是⊙O的直径,⊙O交BC于点D,DE⊥AC于点E,BE交⊙O于点F,连接AF,AF的延长线交DE于点P.
(1)求证:DE是⊙O的切线;
(2)求tan∠ABE的值;
(3)若OA=2,求线段AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,过点B的直线与对角线AC、边AD分别交于点E和F.过点E作EG∥BC,交AB于G,则图中相似三角形有( )

A. 4对B. 5对C. 6对D. 7对
查看答案和解析>>
科目:初中数学 来源: 题型:
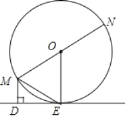
【题目】已知:如图,MN为⊙O的直径,ME是⊙O的弦,MD垂直于过点E的直线DE,垂足为点D,且ME平分∠DMN.
求证:(1)DE是⊙O的切线;
(2)ME2=MDMN.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com