
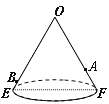
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为6 cm,母线OE(OF)长为9cm.在母线OF上的点A处有一块爆米花残渣,且FA = 3cm.在母线OE上的点B处有一只蚂蚁,且EB = 1cm.这只蚂蚁从点B处沿圆锥表面爬行到A点,则爬行的最短距离为 cm.
【答案】![]() .
.
【解析】
试题最短距离的问题首先应转化为圆锥的侧面展开图的问题,转化为平面上两点间的距离的问题.需先算出圆锥侧面展开图的扇形半径.看如何构成一个直角三角形,然后根据勾股定理进行计算.
试题解析:如图,过点A作AH⊥OB于H.

∵OE=OF=9cm,FA=3cm,EB=1cm,
∴OA=6cm,OB=8cm.
圆锥的底面周长是π×6=6π,则6π=![]() ,
,
∴n=120°,
即圆锥侧面展开图的圆心角是120°.
∴∠EOF=60°,
∴AH=OAsin60°=6×![]() (cm),OH=OAcos60°=6×
(cm),OH=OAcos60°=6×![]() =3(cm),
=3(cm),
∴BH=OB-OH=5cm,
∴在直角△ABH中,由勾股定理得到:AB=![]() (cm).
(cm).


科目:初中数学 来源: 题型:
【题目】某服装厂每天生产![]() 、
、![]() 两种品牌的服装共600件,
两种品牌的服装共600件,![]() 、
、![]() 两种品牌的服装每件的成本和利润如右表:
两种品牌的服装每件的成本和利润如右表:
A | B | |
成本(元/件) | 50 | 35 |
利润(元/件) | 20 | 15 |
设每天生产![]() 种品牌服装
种品牌服装![]() 件,每天两种服装获利
件,每天两种服装获利![]() 元.
元.
(1)请写出![]() 关于
关于![]() 的函数关系式;
的函数关系式;
(2)如果服装厂每天至少投入成本26400元,那么每天至少获利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
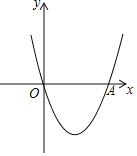
【题目】如图,已知抛物线![]() 过原点且与x轴交于点A,顶点的纵坐标是
过原点且与x轴交于点A,顶点的纵坐标是![]() .
.
![]() 求抛物线的函数表达式及点A坐标;
求抛物线的函数表达式及点A坐标;
![]() 根据图象回答:当x为何值时抛物线位于x轴上方?
根据图象回答:当x为何值时抛物线位于x轴上方?
![]() 直接写出所求抛物线先向左平移3个单位,再向上平移5个单位所得到抛物线的函数表达式.
直接写出所求抛物线先向左平移3个单位,再向上平移5个单位所得到抛物线的函数表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
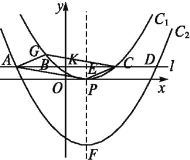
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,![]() 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AC是⊙O的直径,BC是⊙O的弦,点P是⊙O外一点,连接PA、PB、AB、OP,已知PB是⊙O的切线.
(1)求证:∠PBA=∠C;
(2)若OP∥BC,且OP=9,⊙O的半径为3![]() ,求BC的长.
,求BC的长.
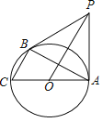
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个学生荡秋千,秋千链子的长度为![]() ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是
,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是![]() ,则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.(结果可以保留根号)
,则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.(结果可以保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
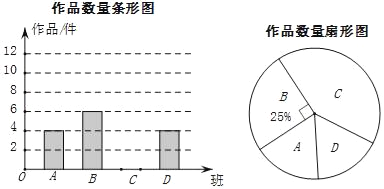
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车远动员甲准备参加一项国际自行车赛事,为此特地骑自行车从A地出发,匀速前往168千米外的B地进行拉练.出发2小时后,乙发现他忘了带某训练用品,于是马上骑摩托车从A地出发匀速去追甲送该用品.已知乙骑摩托车的速度比甲骑自行车的速度每小时多30千米,但摩托车行驶一小时后突遇故障,修理15分钟后,又上路追甲,但速度减小了![]() ,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
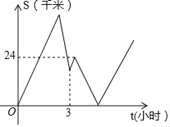
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC=2,∠BAC=45°.将△ABC绕点A逆时针旋转α度(0<α<180)得到△ADE,B,C两点的对应点分别为点D,E,BD,CE所在直线交于点F.
(1)当△ABC旋转到图1位置时,∠CAD= (用α的代数式表示),∠BFC的度数为 °;
(2)当α=45时,在图2中画出△ADE,并求此时点A到直线BE的距离.
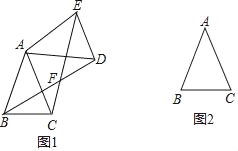
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com