
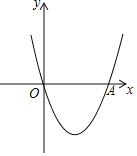
【题目】如图,已知抛物线![]() 过原点且与x轴交于点A,顶点的纵坐标是
过原点且与x轴交于点A,顶点的纵坐标是![]() .
.
![]() 求抛物线的函数表达式及点A坐标;
求抛物线的函数表达式及点A坐标;
![]() 根据图象回答:当x为何值时抛物线位于x轴上方?
根据图象回答:当x为何值时抛物线位于x轴上方?
![]() 直接写出所求抛物线先向左平移3个单位,再向上平移5个单位所得到抛物线的函数表达式.
直接写出所求抛物线先向左平移3个单位,再向上平移5个单位所得到抛物线的函数表达式.
科目:初中数学 来源: 题型:
【题目】如图,己知点A是双曲线y=kx-1(k>0)上的一个动点,连AO并延长交另一分支于点B,以AB为边作等边△ABC,点C在第四象限.随着点A的运动,点C的位置也不断变化,但点C始终在双曲线y=mx-1(m<0)上运动,则m与k的关系是( )

A. m= -kB. m=![]() kC. m= -2kD. m= -3k
kC. m= -2kD. m= -3k
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在宣传“民族团结”活动中,采用四种宣传形式:A.器乐,B.舞蹈,C.朗诵,D.唱歌.每名学生从中选择并且只能选择一种最喜欢的,学校就宣传形式对学生进行了抽样调查,并将调查结果绘制了如下两幅不完整的统计图.

请结合图中所给信息,解答下列问题:
(1)本次调查的学生共有_____人;
(2)补全条形统计图;
(3)该校共有1200名学生,请估计选择“唱歌”的学生有多少人?
(4)七年一班在最喜欢“器乐”的学生中,有甲、乙、丙、丁四位同学表现优秀,现从这四位同学中随机选出两名同学参加学校的器乐队,请用列表或画树状图法求被选取的两人恰好是甲和乙的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《山西省新能源汽车产业2018年行动计划》指出,2018年全省新能源汽车产能将达到30万辆,按照“十三五”规划,到2020年,全省新能源汽车产能将达到41万辆,若设这两年全省新能源汽车产能的平均增长率为![]() ,则根据题意可列出方程是()
,则根据题意可列出方程是()
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】社区利用一块矩形空地建了一个小型的惠民停车场,其布局如图所示.已知停车场的长为52米,宽为28米,阴影部分设计为停车位,要铺花砖,其余部分是等宽的通道.已知铺花砖的面积为640平方米.
(1)求通道的宽是多少米?
(2)该停车场共有车位64个,据调查分析,当每个车位的月租金为200元时,可全部租出;当每个车位的月租金每上涨10元,就会少租出1个车位.当每个车位的月租金上涨多少元时,停车场的月租金收入为14400元?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形OAA1的直角边OA在x轴上,点A1在第一象限,且OA=1,以点A1为直角顶点,OA1为一直角边作等腰直角三角形OA1A2,再以点A2为直角顶点,OA2为直角边作等腰直角三角形OA2A3…依此规律,则点A2018的坐标是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
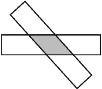
【题目】如图,将两张长为5,宽为1的矩形纸条交叉,让两个矩形对角线交点重合,且使重叠部分成为一个菱形.当两张纸条垂直时,菱形周长的最小值是4,把一个矩形绕两个矩形重合的对角线交点旋转一定角度,在旋转过程中,得出所有重叠部分为菱形的四边形中,周长的最大值是( )
A. 8B. 10C. 10.4D. 12
查看答案和解析>>
科目:初中数学 来源: 题型:
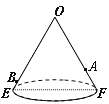
【题目】如图是一个用来盛爆米花的圆锥形纸杯,纸杯开口圆的直径EF长为6 cm,母线OE(OF)长为9cm.在母线OF上的点A处有一块爆米花残渣,且FA = 3cm.在母线OE上的点B处有一只蚂蚁,且EB = 1cm.这只蚂蚁从点B处沿圆锥表面爬行到A点,则爬行的最短距离为 cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,可以自由转动的转盘被它的两条直径分成了四个分别标有数字的扇形区域,其中标有数字“1”的扇形圆心角为120°.转动转盘,待转盘自动停止后,指针指向一个扇形的内部,则该扇形内的数字即为转出的数字,此时,称为转动转盘一次(若指针指向两个扇形的交线,则不计转动的次数,重新转动转盘,直到指针指向一个扇形的内部为止)
(1)转动转盘一次,求转出的数字是-2的概率;
(2)转动转盘两次,用树状图或列表法求这两次分别转出的数字之积为正数的概率.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com