
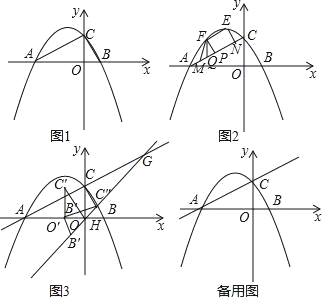
【题目】如图1,抛物线y=﹣![]() 与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
(1)求线段AC的长;
(2)如图2,E为抛物线的顶点,F为AC上方的抛物线上一动点,M、N为直线AC上的两动点(M在N的左侧),且MN=4,作FP⊥AC于点P,FQ∥y轴交AC于点Q.当△FPQ的面积最大时,连接EF、EN、FM,求四边形ENMF周长的最小值.
(3)如图3,将△BCO沿x轴负方向平移![]() 个单位后得△B'C'O',再将△B'C'O'绕点O'顺时针旋转α度,得到△B″C″O'(其中0°<α<180°),旋转过程中直线B″C″与直线AC交于点G,与x轴交于点H,当△AGH是等腰三角形时,求α的度数.
个单位后得△B'C'O',再将△B'C'O'绕点O'顺时针旋转α度,得到△B″C″O'(其中0°<α<180°),旋转过程中直线B″C″与直线AC交于点G,与x轴交于点H,当△AGH是等腰三角形时,求α的度数.
【答案】(1)6(2)![]() (3)α的值为15°或60°或105°或150°
(3)α的值为15°或60°或105°或150°
【解析】
(1)根据抛物线的解析式求出A,C两点坐标,可得OA=3![]() ,OC=3,利用勾股定理即可解决问题.
,OC=3,利用勾股定理即可解决问题.
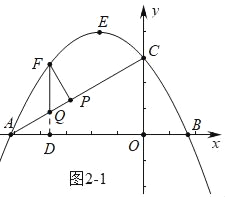
(2)如图2﹣1中,延长FQ交OA于D.设F(m,﹣![]() m2﹣
m2﹣![]() m+3),构建二次函数求出FQ的值最大时的点F的坐标,如图2﹣2中,作FF′∥AC,使得FF′=MN=4,作点F′关于直线AC的对称点F″,连接FF″交直线AC于点M,连接FM,EN,EF,此时四边形ENMF的周长最短.再求出点M.N的坐标即可解决问题.
m+3),构建二次函数求出FQ的值最大时的点F的坐标,如图2﹣2中,作FF′∥AC,使得FF′=MN=4,作点F′关于直线AC的对称点F″,连接FF″交直线AC于点M,连接FM,EN,EF,此时四边形ENMF的周长最短.再求出点M.N的坐标即可解决问题.
(3)分四种情形分别画出图象求解即可.
(1)由题意:A(﹣3![]() ,0),B(
,0),B(![]() ,0),C(0,3),
,0),C(0,3),
∴OA=3![]() ,OC=3,
,OC=3,
∴AC=![]() =6.
=6.
(2)如图2﹣1中,延长FQ交OA于D.设F(m,﹣![]() m2﹣
m2﹣![]() m+3),
m+3),
∵tan∠CAO=![]() =
=![]() ,
,
∴∠CAO=30°,∵FQ∥y轴,FP⊥AC,
∴∠ADQ=∠FPQ=90°,
∴∠AQD=∠FQP=60°,
∴当FQ最大时,△FPQ的面积最大,
∵直线AC的解析式为y=![]() x+3,
x+3,
∴Q(m,![]() m+3),
m+3),
∴FQ=﹣![]() m2﹣
m2﹣![]() m+3﹣
m+3﹣![]() m﹣3=﹣
m﹣3=﹣![]() m2﹣
m2﹣![]() m=﹣
m=﹣![]() (m+
(m+![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴m=﹣![]() ,FQ的值最大,即△PFQ的面积最大,此时F(﹣
,FQ的值最大,即△PFQ的面积最大,此时F(﹣![]() ,
,![]() ),
),
如图2﹣2中,作FF′∥AC,使得FF′=MN=4,作点F′关于直线AC的对称点F″,连接FF″交直线AC于点M,连接FM,EN,EF,此时四边形ENMF的周长最短.
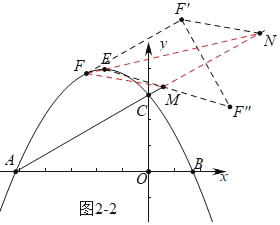
由题意点F向右平移2![]() 个单位,再向上平移2个单位得到点F′(
个单位,再向上平移2个单位得到点F′(![]() ,
,![]() ),
),
∵F″与F′关于直线AC对称,
∴F″(![]() ,
,![]() ),
),
∴M(![]() ),N(
),N(![]() ),
),
∵抛物线顶点E(﹣![]() ,4),
,4),
∴FM=![]() ,EN=
,EN=![]() =
=![]() ,EF=
,EF=![]() =
=![]() ,
,
∴四边形ENMF的周长的最小值为![]() .
.
(3)①如图3﹣1中,当AG=AH时
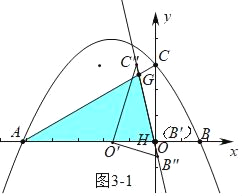
∵AG=AH,∠HAG=30°,
∴∠AHG=∠AGH=75°,
∵∠AHG=∠HO′B″+∠O′B″H,∠O′B″H=60°
∴∠HO′B″=15°,
∴α=15°
②如图3﹣2中,当HA=HG时,
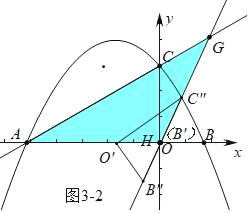
∵AG∥O′C″,
∴∠HO′C″=∠GAO=30°,
∴∠HO′B″=60°,
∴α=60°.
③如图3﹣3中,当AG=AH时,
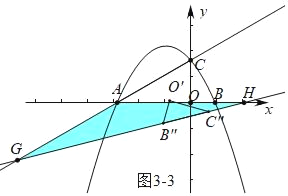
∵∠AGH=∠AHG=15°,
∵∠O′C″B″=∠C″O′H+∠AHG,
∴∠HO′C″=15°,
∴∠HO′B″=105°,
∴α=105°.
④如图3﹣4中,当GA=GH时,同法可得∠OO′B″=150°,α=150°.
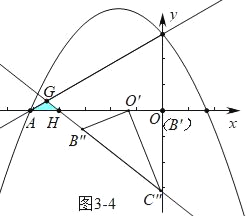
综上所述,满足条件的α的值为15°或60°或105°或150°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
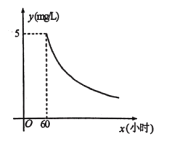
【题目】《城镇污水处理厂污染物排放标准》中硫化物的排放标准为![]() .某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为
.某污水处理厂在自查中发现,所排污水中硫化物浓度超标,因此立即整改,并开始实时监测.据监测,整改开始第60小时时,所排污水中硫化物的浓度为![]() ;从第60小时开始,所排污水中硫化物的浓度
;从第60小时开始,所排污水中硫化物的浓度![]() 是监测时间
是监测时间![]() (小时)的反比例函数,其图象如图所示。
(小时)的反比例函数,其图象如图所示。
(1)求![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)整改开始第100小时时,所排污水中硫化物浓度为_____![]() ;
;
(3)按规定所排污水中硫化物的浓度不超过![]() 时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?
时,才能解除实时监测,此次整改实时监测的时间至少为多少小时?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个学生荡秋千,秋千链子的长度为![]() ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是
,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是![]() ,则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.(结果可以保留根号)
,则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.(结果可以保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
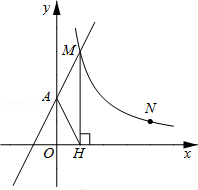
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自行车远动员甲准备参加一项国际自行车赛事,为此特地骑自行车从A地出发,匀速前往168千米外的B地进行拉练.出发2小时后,乙发现他忘了带某训练用品,于是马上骑摩托车从A地出发匀速去追甲送该用品.已知乙骑摩托车的速度比甲骑自行车的速度每小时多30千米,但摩托车行驶一小时后突遇故障,修理15分钟后,又上路追甲,但速度减小了![]() ,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
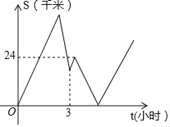
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天晚上,李明利用灯光下的影子长来测量一路灯D的高度.如图,当在点A处放置标杆时,李明测得直立的标杆高AM与影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处放置同一个标杆,测得直立标杆高BN的影子恰好是线段AB,并测得AB=1.2m,已知标杆直立时的高为1.8m,求路灯的高CD的长.
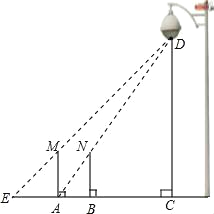
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图中的方格图均是由边长为1的小正方形组成的,现通过图形变换将图1中阴影部分的图形割补成一个正方形。其思想方法是:由于要拼成的正方形的面积为“5”(由5个小正方形组成),则正方形的边长为![]() ,而
,而![]() =
=![]() 。因此,具体做法是:①连结A1A3、A1A5;②将△A1A2A3绕A3沿顺时针方向旋转90°;③将△A1A5A6绕A5沿逆时针方向旋转90°;④将小正方形A1A6A7A8先向左平移2个单位,再向上平移1个单位。图中四边形A1A3A4A5即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求:直接在图上画出图形,并写出一种具体做法。)
。因此,具体做法是:①连结A1A3、A1A5;②将△A1A2A3绕A3沿顺时针方向旋转90°;③将△A1A5A6绕A5沿逆时针方向旋转90°;④将小正方形A1A6A7A8先向左平移2个单位,再向上平移1个单位。图中四边形A1A3A4A5即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求:直接在图上画出图形,并写出一种具体做法。)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司从2009年开始投入技术改造资金,经技术改进后,其产品的生产成本不断降低,具体数据如表:
年度 | 2009 | 2010 | 2011 | 2012 |
投入技改资金x(万元) | 2.5 | 3 | 4 | 4.5 |
产品成本y(万元/件) | 7.2 | 6 | 4.5 | 4 |
(1)试判断:从上表中的数据看出,y与x符合你学过的哪个函数模型?请说明理由,并写出它的解析式.
(2)按照上述函数模型,若2013年已投入技改资金5万元
①预计生产成本每件比2012年降低多少元?
②如果打算在2013年把每件产品的成本降低到3.2万元,则还需投入技改资金多少万元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com