
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
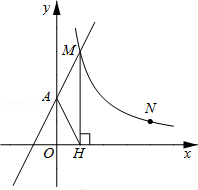
【答案】解:(1)由y=2x+2可知A(0,2),即OA=2。
∵tan∠AHO=2,∴OH=1。
∵MH⊥x轴,∴点M的横坐标为1。
∵点M在直线y=2x+2上,
∴点M的纵坐标为4.即M(1,4)。
∵点M在![]() 上,∴k=1×4=4。
上,∴k=1×4=4。
(2)存在。
∵点N(a,1)在反比例函数![]() (x>0)上,
(x>0)上,
∴a=4.即点N的坐标为(4,1)。
过点N作N关于x轴的对称点N1,连接MN1,交x轴于P(如图所示)。
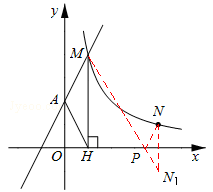
此时PM+PN最小。
∵N与N1关于x轴的对称,N点坐标为(4,1),∴N1的坐标为(4,﹣1)。
设直线MN1的解析式为y=kx+b。
由![]() 解得
解得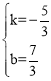 。
。
∴直线MN1的解析式为![]() 。
。
令y=0,得x=![]() .
.
∴P点坐标为(![]() ,0)。
,0)。
【解析】(1)根据直线解析式求A点坐标,得OA的长度;根据三角函数定义可求OH的长度,得点M的横坐标;根据点M在直线上可求点M的坐标.从而可求K的值;
(2)根据反比例函数解析式可求N点坐标;作点N关于x轴的对称点N1,连接MN1与x轴的交点就是满足条件的P点位置:
根据轴对称的性质,线段中垂线的性质和三角形三边关系,对x轴上任一点P1,总有
P1M+P1N>MN1=PM+PN。


科目:初中数学 来源: 题型:
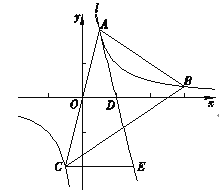
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
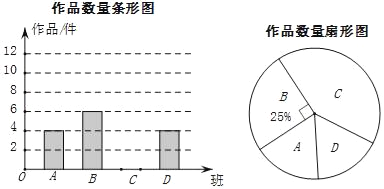
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,O为坐标原点,四边形OABC为矩形,A(20,0),C(0,8),点D是OA的中点,点P在边BC上运动,当△ODP是腰长为10的等腰三角形时,则P点的坐标为_____.
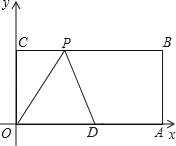
查看答案和解析>>
科目:初中数学 来源: 题型:
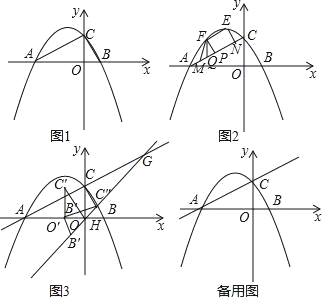
【题目】如图1,抛物线y=mx2﹣4mx+3m(m>0)与x轴交于A,B两点(点B在点A右侧).与y轴交点C,与直线l:y=x+1交于D、E两点,
(1)当m=1时,连接BC,求∠OBC的度数;
(2)在(1)的条件下,连接DB、EB,是否存在抛物线在第四象限上一点P,使得S△DBE=S△DPE?若存在,求出此时P点坐标及PB的长度;若不存在,请说明理由;
(3)若以DE为直径的圆恰好与x轴相切,求此时m的值.
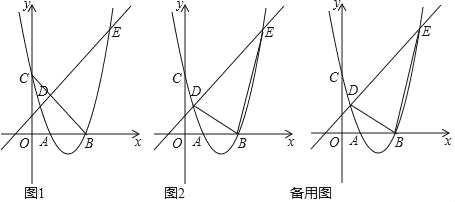
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,已知抛物线y=﹣x2+bx+c交y轴于点A(0,4),交x轴于点B(4,0),点P是抛物线上一动点,过点P作x轴的垂线PQ,过点A作AQ⊥PQ于点Q,连接AP.
(1)填空:抛物线的解析式为 ,点C的坐标 ;
(2)点P在抛物线上运动,若△AQP∽△AOC,求点P的坐标;
(3)如图2,当点P位于抛物线的对称轴的右侧,若将△APQ沿AP对折,点Q的对应点为点Q',请直接写出当点Q'落在坐标轴上时点P的坐标.
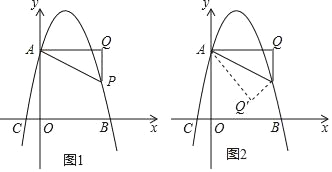
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=﹣![]() 与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
与x轴交于A、B两点,与y轴交于点C,连接AC、BC.
(1)求线段AC的长;
(2)如图2,E为抛物线的顶点,F为AC上方的抛物线上一动点,M、N为直线AC上的两动点(M在N的左侧),且MN=4,作FP⊥AC于点P,FQ∥y轴交AC于点Q.当△FPQ的面积最大时,连接EF、EN、FM,求四边形ENMF周长的最小值.
(3)如图3,将△BCO沿x轴负方向平移![]() 个单位后得△B'C'O',再将△B'C'O'绕点O'顺时针旋转α度,得到△B″C″O'(其中0°<α<180°),旋转过程中直线B″C″与直线AC交于点G,与x轴交于点H,当△AGH是等腰三角形时,求α的度数.
个单位后得△B'C'O',再将△B'C'O'绕点O'顺时针旋转α度,得到△B″C″O'(其中0°<α<180°),旋转过程中直线B″C″与直线AC交于点G,与x轴交于点H,当△AGH是等腰三角形时,求α的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示:
用电量(千瓦时) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数、平均数分别是( )
A. 180,160,164B. 160,180;164
C. 160,160,164D. 180,180,164
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AD是高,矩形PQMN的顶点P、N分别在AB、AC上,QM在边BC上,若BC=8cm,AD=6cm,且PN=2PQ,则矩形PQMN的周长为( )
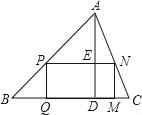
A. 14.4cmB. 7.2cmC. 11.52cmD. 12.4cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com