
【题目】某课外小组的同学们在社会实践活动中调查了20户家庭莱月的用电量,如表所示:
用电量(千瓦时) | 120 | 140 | 160 | 180 | 200 |
户数 | 2 | 3 | 6 | 7 | 2 |
则这20户家庭该月用电量的众数和中位数、平均数分别是( )
A. 180,160,164B. 160,180;164
C. 160,160,164D. 180,180,164
 教材全解字词句篇系列答案
教材全解字词句篇系列答案科目:初中数学 来源: 题型:
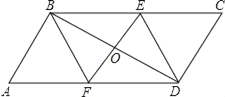
【题目】如图,在平行四边形ABCD中,过对角线BD中点的直线交AD、BC边于F、E.
(1)求证:四边形BEDF是平行四边形;
(2)当四边形BEDF是菱形时,写出EF与BD的关系.
(3)若∠A=60°,AB=4,BC=6,四边形BEDF是矩形,求该矩形的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
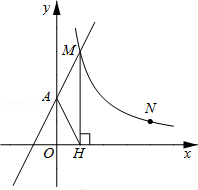
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
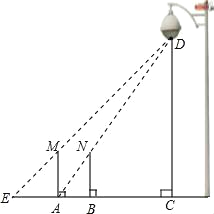
【题目】一天晚上,李明利用灯光下的影子长来测量一路灯D的高度.如图,当在点A处放置标杆时,李明测得直立的标杆高AM与影子长AE正好相等,接着李明沿AC方向继续向前走,走到点B处放置同一个标杆,测得直立标杆高BN的影子恰好是线段AB,并测得AB=1.2m,已知标杆直立时的高为1.8m,求路灯的高CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图中的方格图均是由边长为1的小正方形组成的,现通过图形变换将图1中阴影部分的图形割补成一个正方形。其思想方法是:由于要拼成的正方形的面积为“5”(由5个小正方形组成),则正方形的边长为![]() ,而
,而![]() =
=![]() 。因此,具体做法是:①连结A1A3、A1A5;②将△A1A2A3绕A3沿顺时针方向旋转90°;③将△A1A5A6绕A5沿逆时针方向旋转90°;④将小正方形A1A6A7A8先向左平移2个单位,再向上平移1个单位。图中四边形A1A3A4A5即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求:直接在图上画出图形,并写出一种具体做法。)
。因此,具体做法是:①连结A1A3、A1A5;②将△A1A2A3绕A3沿顺时针方向旋转90°;③将△A1A5A6绕A5沿逆时针方向旋转90°;④将小正方形A1A6A7A8先向左平移2个单位,再向上平移1个单位。图中四边形A1A3A4A5即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求:直接在图上画出图形,并写出一种具体做法。)


查看答案和解析>>
科目:初中数学 来源: 题型:
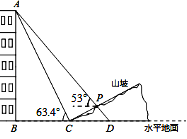
【题目】如图,某人在山坡坡脚C处测得一座建筑物顶点A的仰角为63.4°,沿山坡向上走到P处再测得该建筑物顶点A的仰角为53°.已知BC=90米,且B、C、D在同一条直线上,山坡坡度i=5:12.
(1)求此人所在位置点P的铅直高度.(结果精确到0.1米)
(2)求此人从所在位置点P走到建筑物底部B点的路程(结果精确到0.1米)
(测倾器的高度忽略不计,参考数据:tan53°≈![]() ,tan63.5°≈2)
,tan63.5°≈2)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知正方形ABCD的边长为6,E,F分别是AB、BC边上的点,且∠EDF=45°,将△DAE绕点D逆时针旋转90°,得到△DCM.

(1)求证:EF=MF;
(2)若AE=2,求FC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
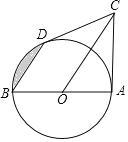
【题目】如图,AB是⊙O的直径,CD切⊙O于点D,且BD∥OC,连接AC.
(1)求证:AC是⊙O的切线;
(2)若AB=OC=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一个三角形,设其三个内角的度数分别为x°、y°和z°,若x、y、z满足x2+y2=z2,我们定义这个三角形为美好三角形.
(1)△ABC中,若∠A=40°,∠B=80°,则△ABC (填“是”或“不是”)美好三角形;
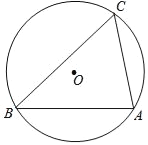
(2)如图,锐角△ABC是⊙O的内接三角形,∠C=60°,AC=2,⊙O的直径是2![]() ,求证:△ABC是美好三角形;
,求证:△ABC是美好三角形;
(3)已知△ABC是美好三角形,∠A=30°,求∠C的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com