
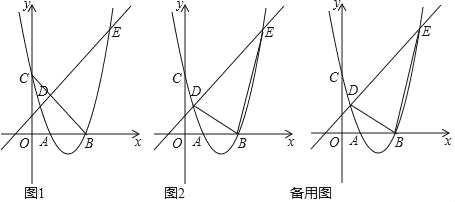
【题目】如图1,抛物线y=mx2﹣4mx+3m(m>0)与x轴交于A,B两点(点B在点A右侧).与y轴交点C,与直线l:y=x+1交于D、E两点,
(1)当m=1时,连接BC,求∠OBC的度数;
(2)在(1)的条件下,连接DB、EB,是否存在抛物线在第四象限上一点P,使得S△DBE=S△DPE?若存在,求出此时P点坐标及PB的长度;若不存在,请说明理由;
(3)若以DE为直径的圆恰好与x轴相切,求此时m的值.
【答案】(1)∠OBC=45°;(2)存在,P(2,﹣1),BP=![]() ;(3)m=
;(3)m=![]() 或﹣
或﹣![]() .
.
【解析】
(1)抛物线y=mx2-4mx+3m=m(x2-4x+3)=m(x-1)(x-3),把当m=1代入即可求解;
(2)S△DBE=S△DPE,∴点B、点P到直线DE的距离相等即可求解;
(3)求出DE的中点坐标为(![]() ,
,![]() ),即DE的长度,则圆的半径=
),即DE的长度,则圆的半径=![]() DE,利用
DE,利用![]() =
=![]() DE,即可求解.
DE,即可求解.
(1)∵抛物线y=mx2﹣4mx+3m=m(x2﹣4x+3)=m(x﹣1)(x﹣3),
∴A(1,0),B(3,0),
∴OB=3,
当m=1时,抛物线解析式为y=x2﹣4x+3,
∴C(0,3),∴OC=3,
∴OB=OC,在Rt△OBC中,∠BOC=90°,
∴∠OBC=45°;
(2)∵S△DBE=S△DPE,
∴点B、点P到直线DE的距离相等,即可求解,
∴BP∥DE,
由(1)知,B(3,0),
∵直线DE的解析式为y=x+1,
∴直线BP的解析式为y=x﹣3①,
∵抛物线解析式为y=x2﹣4x+3②,
联立①②解得,![]() 或
或![]() (点B的坐标,舍去),
(点B的坐标,舍去),
∴P(2,﹣1),
∵B(3,0),
∴BP=![]() =
=![]() ;
;
(3)∵点D,E在直线y=x+1上,
∴设D(x1,y1),E(x2,y2),
∵抛物线y=mx2﹣4mx+3m…③,
直线l:y=x+1…④,
联立③④得,mx2﹣4mx+3m=x+1,
∴mx2﹣(4m+1)x+(3m﹣1)=0,
∴x1+x2=![]() ,x1x2=
,x1x2=![]() ,
,
∴y1+y2=x1+x2+2=![]() ,
,
∴DE的中点坐标为(![]() ,
,![]() ),
),
DE=![]() =
=![]() =
=![]() =
=![]() ,
,
∵以DE为直径的圆恰好与x轴相切,
∴圆的半径=![]() DE,
DE,
则:![]() =
=![]()
![]() ,
,
整理得:28m2﹣12m﹣1=0,
解得:m=![]() 或﹣
或﹣![]() .
.


科目:初中数学 来源: 题型:
【题目】綦江中学新校区建设正按计划顺利推进,其中有一块矩形地面准备用同样规格的黑、白两色的正方形瓷砖按如图所示的设计进行铺设,请观察下列图形并解答有关问题.
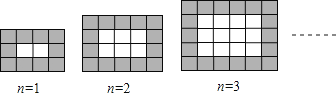
![]() 第n个图中共有块瓷砖
第n个图中共有块瓷砖![]() 用含n的代数式表示
用含n的代数式表示![]() ;
;
![]() 按上述铺设方案,铺这块矩形地面共用了506块瓷砖,求此时n的值;
按上述铺设方案,铺这块矩形地面共用了506块瓷砖,求此时n的值;
![]() 是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
是否存在黑瓷砖与白瓷砖块数相等的情形?请通过计算说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知顶点为P的抛物线C1的解析式为y=a(x-3)2(a≠0),且经过点(0,1).
(1)求a的值及抛物线C1的解析式;
(2)如图,将抛物线C1向下平移h(h>0)个单位得到抛物线C2,过点K(0,m2)(m>0)作直线l平行于x轴,与两抛物线从左到右分别相交于A,B,C,D四点,且A,C两点关于y轴对称.
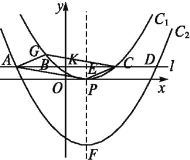
①点G在抛物线C1上,当m为何值时,四边形APCG为平行四边形?
②若抛物线C1的对称轴与直线l交于点E,与抛物线C2交于点F.试探究:在K点运动过程中,![]() 的值是否改变?若会,请说明理由;若不会,请求出这个值.
的值是否改变?若会,请说明理由;若不会,请求出这个值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个学生荡秋千,秋千链子的长度为![]() ,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是
,当秋千向两边摆动时,摆角(指摆到最高位置时的秋千与铅垂线的夹角)恰好是![]() ,则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.(结果可以保留根号)
,则它摆至最高位置时与其摆至最低位置时的高度之差为 ____m.(结果可以保留根号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】济南某中学在参加“创文明城,点赞泉城”书画比赛中,杨老师从全校30个班中随机抽取了4个班(用A,B,C,D表示),对征集到的作鼎的数量进行了分析统计,制作了两幅不完整的统计图.
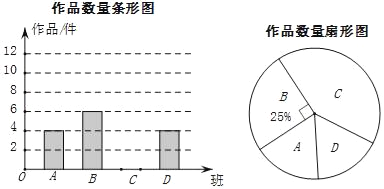
请根据以上信息,回答下列问题:
(l)杨老师采用的调查方式是 (填“普查”或“抽样调查”);
(2)请补充完整条形统计图,并计算扇形统计图中C班作品数量所对应的圆心角度数 .
(3)请估计全校共征集作品的什数.
(4)如果全枝征集的作品中有5件获得一等奖,其中有3名作者是男生,2名作者是女生,现要在获得一样等奖的作者中选取两人参加表彰座谈会,请你用列表或树状图的方法,求恰好选取的两名学生性别相同的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
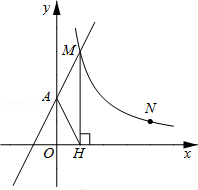
【题目】如图,直线y=2x+2与y轴交于A点,与反比例函数![]() (x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(x>0)的图象交于点M,过M作MH⊥x轴于点H,且tan∠AHO=2.
(1)求k的值;
(2)点N(a,1)是反比例函数![]() (x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
(x>0)图象上的点,在x轴上是否存在点P,使得PM+PN最小?若存在,求出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
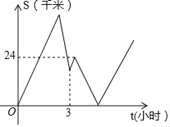
【题目】自行车远动员甲准备参加一项国际自行车赛事,为此特地骑自行车从A地出发,匀速前往168千米外的B地进行拉练.出发2小时后,乙发现他忘了带某训练用品,于是马上骑摩托车从A地出发匀速去追甲送该用品.已知乙骑摩托车的速度比甲骑自行车的速度每小时多30千米,但摩托车行驶一小时后突遇故障,修理15分钟后,又上路追甲,但速度减小了![]() ,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
,乙追上甲交接了训练用品(交接时间忽略不计),随后立即以修理后的速度原路返回,甲继续以原来的速度骑行直至B地.如图表示甲、乙两人之间的距离S(千米)与甲骑行的时间t(小时)之间的部分图象,则当甲达到B地时,乙距离A地_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图中的方格图均是由边长为1的小正方形组成的,现通过图形变换将图1中阴影部分的图形割补成一个正方形。其思想方法是:由于要拼成的正方形的面积为“5”(由5个小正方形组成),则正方形的边长为![]() ,而
,而![]() =
=![]() 。因此,具体做法是:①连结A1A3、A1A5;②将△A1A2A3绕A3沿顺时针方向旋转90°;③将△A1A5A6绕A5沿逆时针方向旋转90°;④将小正方形A1A6A7A8先向左平移2个单位,再向上平移1个单位。图中四边形A1A3A4A5即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求:直接在图上画出图形,并写出一种具体做法。)
。因此,具体做法是:①连结A1A3、A1A5;②将△A1A2A3绕A3沿顺时针方向旋转90°;③将△A1A5A6绕A5沿逆时针方向旋转90°;④将小正方形A1A6A7A8先向左平移2个单位,再向上平移1个单位。图中四边形A1A3A4A5即是所求作的正方形。仿照此方法将图2中的阴影部分的图形割补成正方形。(要求:直接在图上画出图形,并写出一种具体做法。)


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在矩形ABCD中,点E在AD上,EC平分∠BED.
(1)试判断△BEC是否为等腰三角形,并说明理由.
(2)若AB=1,∠ABE=45°,求BC的长.
(3)在原图中画△FCE,使它与△BEC关于CE的中点O成中心对称,此时四边形BCFE是什么特殊平行四边形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com