
【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).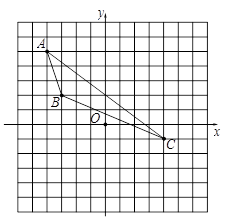
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高.
【答案】
(1)解: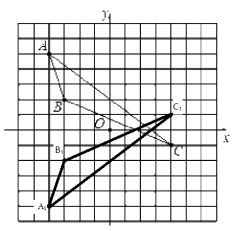 如图所示,△A1B1C1即为所求。
如图所示,△A1B1C1即为所求。
(2)解:A1(-4, -5),B1(﹣3,- 2),C1(4,1)
(3)解: 由图可得S△ABC=6×8×![]() -1×3×
-1×3×![]() -1×3-3×7×
-1×3-3×7×![]() =9
=9
又AC=![]() =10
=10
∵![]() AC×h=S△ABC
AC×h=S△ABC
∴h=9×2÷10=1.8
所以△ABC的AC边上的高为1.8![]()
【解析】(1)(2)中由关于X轴对称变换的性质易得A1(-4, -5),B1(﹣3,- 2),C1(4,1),在坐标系内,描点,连线即可。
可利用割补法计算出三角形ABC的面积,再利用勾股定理得AC的长,最后利用面积关系计算得到AC边上的高。
【考点精析】认真审题,首先需要了解坐标与图形变化-对称(关于x轴对称的点的特征:两个点关于x轴对称时,它们的坐标中,x相等,y的符号相反,即点P(x,y)关于x轴的对称点为P’(x,-y);关于y轴对称的点的特征:两个点关于y轴对称时,它们的坐标中,y相等,x的符号相反,即点P(x,y)关于y轴的对称点为P’(-x,y)).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
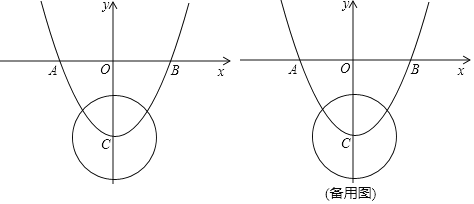
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点与
两点与![]() 轴交于点
轴交于点![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 为⊙
为⊙![]() 上一动点.
上一动点.
(1)点![]() 的坐标分别为
的坐标分别为![]() ( ),
( ),![]() ( );
( );
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,若
,若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的最大值= .
的最大值= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点A,与y轴交于点C,抛物线
与x轴交于点A,与y轴交于点C,抛物线![]() 经过A、C两点,与x轴的另一交点为点B.
经过A、C两点,与x轴的另一交点为点B.
(1)求抛物线的函数表达式;
(2)点D为直线AC上方抛物线上一动点;
①连接BC、CD,设直线BD交线段AC于点E,△CDE的面积为![]() ,△BCE的面积为
,△BCE的面积为![]() ,求
,求![]() 的最大值;
的最大值;
②过点D作DF⊥AC,垂足为点F,连接CD,是否存在点D,使得△CDF中的某个角恰好等于∠BAC的2倍?若存在,求点D的横坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
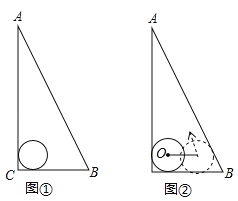
【题目】如图,△ABC是一块直角三角板,且∠C=90°,∠A=30°,现将圆心为点O的圆形纸片放置在三角板内部.
(1)如图①,当圆形纸片与两直角边AC、BC都相切时,试用直尺与圆规作出射线CO;(不写作法与证明,保留作图痕迹)
(2)如图②,将圆形纸片沿着三角板的内部边缘滚动1周,回到起点位置时停止,若BC=9,圆形纸片的半径为2,求圆心O运动的路径长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为了解全校学生对新闻、体育、动画、娱乐、戏曲五类电视节目的喜爱情况,随机选取该校部分学生进行调查,要求每名学生从中只选一类最喜爱的电视节目.以下是根据调查结果绘制的统计图表的一部分.
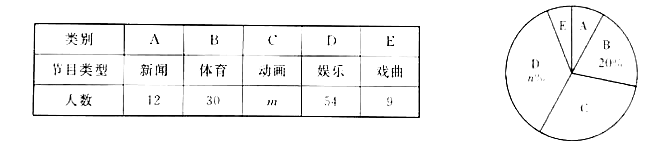
根据以上信息,解答下列问题:
(1)被调查的学生中,最喜爱体育节目的有 人,这些学生数占被调查总人数的百分比为 %;
(2)被调查学生的总数为 人,统计表中![]() 的值为 ,统计图中
的值为 ,统计图中![]() 的值为 ;
的值为 ;
(3)在统计图中,![]() 类所对应扇形圆心角的度数为 ;
类所对应扇形圆心角的度数为 ;
(4)该校共有2000名学生,根据调查结果,估计该校最喜爱欣慰节目的学生数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,四边形![]() 的顶点
的顶点![]() 是坐标原点,点
是坐标原点,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 分别为四边形
分别为四边形![]() 边上的动点,动点
边上的动点,动点![]() 从点
从点![]() 开始,以每秒1个单位长度的速度沿
开始,以每秒1个单位长度的速度沿![]() 路线向中点
路线向中点![]() 匀速运动,动点
匀速运动,动点![]() 从
从![]() 点开始,以每秒两个单位长度的速度沿
点开始,以每秒两个单位长度的速度沿![]() 路线向终点
路线向终点![]() 匀速运动,点
匀速运动,点![]() 同时从
同时从![]() 点出发,当其中一点到达终点后,另一点也随之停止运动。设动点运动的时间
点出发,当其中一点到达终点后,另一点也随之停止运动。设动点运动的时间![]() 秒(
秒(![]() ),
),![]() 的面积为
的面积为![]() .
.
(1)填空:![]() 的长是 ,
的长是 ,![]() 的长是 ;
的长是 ;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)当![]() 时,设点
时,设点![]() 的纵坐标为
的纵坐标为![]() ,求
,求![]() 与
与![]() 的函数关系式;
的函数关系式;
(4)若![]() ,请直接写出此时
,请直接写出此时![]() 的值.
的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com