
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���![]() �Ķ���
�Ķ���![]() ������ԭ�㣬��
������ԭ�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ֱ�Ϊ�ı���
�ֱ�Ϊ�ı���![]() ���ϵĶ��㣬����
���ϵĶ��㣬����![]() �ӵ�
�ӵ�![]() ��ʼ����ÿ��1����λ���ȵ��ٶ���
��ʼ����ÿ��1����λ���ȵ��ٶ���![]() ·�����е�
·�����е�![]() �����˶�������
�����˶�������![]() ��
��![]() �㿪ʼ����ÿ��������λ���ȵ��ٶ���
�㿪ʼ����ÿ��������λ���ȵ��ٶ���![]() ·�����յ�
·�����յ�![]() �����˶�����
�����˶�����![]() ͬʱ��
ͬʱ��![]() �������������һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶����趯���˶���ʱ��
�������������һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶����趯���˶���ʱ��![]() ����
����![]() ����
����![]() �����Ϊ
�����Ϊ![]() .
.
��1����գ�![]() �ij��� ��
�ij��� ��![]() �ij��� ��
�ij��� ��
��2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ʱ�����
ʱ�����![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��4����![]() ����ֱ��д����ʱ
����ֱ��д����ʱ![]() ��ֵ.
��ֵ.

���𰸡�(1)10��6����2��S=6����3��y=![]() ��(4)8��
��(4)8��![]() ��
��![]() .
.
��������
�������������![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ɵ�OA=6,OB=8,���ݹ��ɶ����������AB=10������C��CM
���ɵ�OA=6,OB=8,���ݹ��ɶ����������AB=10������C��CM![]() y���ڵ�M���ɵ�
y���ڵ�M���ɵ�![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ���ɵ� BM=4,CM=2
���ɵ� BM=4,CM=2![]() ,���ɹ��ɶ��������BC=6����2������C��CE
,���ɹ��ɶ��������BC=6����2������C��CE![]() x���ڵ�E���ɵ�
x���ڵ�E���ɵ�![]() ������Ϊ
������Ϊ![]() ���ɵ�CE=4,OE=2
���ɵ�CE=4,OE=2![]() ,��Rt��CEO�У����ݹ��ɶ��������OC=6,��t=3ʱ����N���C�غϣ�OM=3������CM���ɵ�NE=CE=4,����
,��Rt��CEO�У����ݹ��ɶ��������OC=6,��t=3ʱ����N���C�غϣ�OM=3������CM���ɵ�NE=CE=4,����![]() ,��S=6����3����3<t<6ʱ����N���߶�BC�ϣ�BN=12-2t������N��NG
,��S=6����3����3<t<6ʱ����N���߶�BC�ϣ�BN=12-2t������N��NG![]() y���ڵ�G������C��CF
y���ڵ�G������C��CF![]() y���ڵ�F���ɵ�F(0��4)������OF=4,OB=8,������BGN=��BFC=90�������ж�NG
y���ڵ�F���ɵ�F(0��4)������OF=4,OB=8,������BGN=��BFC=90�������ж�NG![]() CF������
CF������![]() ,��
,��![]() ,���BG=8-
,���BG=8-![]() �����ɵ�y =
�����ɵ�y =![]() ����4��������M���߶�OA�ϣ�N���߶�OC��������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���·�������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���Ϸ����������tֵ����.
����4��������M���߶�OA�ϣ�N���߶�OC��������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���·�������M����N�����߶�AB�ϣ��ҵ�M�ڵ�N���Ϸ����������tֵ����.
���������
(1)10��6��
��2����ͼ1������C��CE![]() x���ڵ�E��
x���ڵ�E��
����![]() ������Ϊ
������Ϊ![]() ����CE=4,OE=2
����CE=4,OE=2![]() ,
,
��Rt��CEO��OC=![]() ,
,
��t=3ʱ����N���C�غϣ�OM=3������CM��
��NE=CE=4,
��![]() ,
,
��S=6.
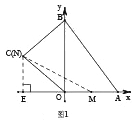
��3����ͼ2����3<t<6ʱ����N���߶�BC�ϣ�BN=12-2t��
����N��NG![]() y���ڵ�G������C��CF
y���ڵ�G������C��CF![]() y���ڵ�F����F(0��4)
y���ڵ�F����F(0��4)
��OF=4,OB=8,
��BF=8-4=4
�ߡ�BGN=��BFC=90����
��NG![]() CF
CF
��![]() ,��
,��![]() ,
,
���BG=8-![]() ��
��
��y=OB-BG=8-(8-![]() )=
)=![]()
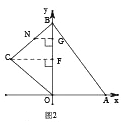
(4)8��![]() ��
��![]() .
.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��![]() ��
��![]() �����ڵ�
�����ڵ�![]() ��
��![]() Ϊ
Ϊ![]() ���ң�
���ң�![]() ��
��![]() ��
��![]() �ཻ�ڵ�
�ཻ�ڵ�![]() ��
��
��1����֤��![]() ��
��
��2����![]() ��
��![]() �����߶�
�����߶�![]() �ij���
�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ����ABC�Ķ���ֱ�ΪA��-4�� 5����B����3�� 2����C��4��-1����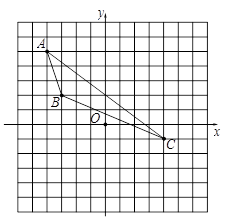
��1��������ABC����x��ԳƵ�ͼ�Ρ�A1B1C1��
��2��д��A1��B1��C1�����ꣻ
��3����AC=10�����ABC��AC���ϵĸߣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ![]() �У�������
�У�������![]() �Ŀ������ϣ��Ҿ�����
�Ŀ������ϣ��Ҿ�����![]() .
.
��1�����������߾�����![]() ������
������![]() ���ཻ�ڵ�
���ཻ�ڵ�![]() .
.
����գ�![]() ���ú�
���ú�![]() �Ĵ���ʽ��ʾ����
�Ĵ���ʽ��ʾ����
����![]() ��ֵ��Сʱ���������ߵĽ���ʽ��
��ֵ��Сʱ���������ߵĽ���ʽ��
��2����![]() ����
����![]() ���������ϵĵ㵽
���������ϵĵ㵽![]() ���������ֵΪ3ʱ����
���������ֵΪ3ʱ����![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��2020��Ϊ����¹����飬ij����Ҫ�˽�ÿһ��¥�ľ�������������Ա�������Խ��з��ߣ�һ־Ը�ߵõ�ij��¥60�������˵����䣨��λ���꣩�������£�62��63��75��79��68��85��82��69��70������������ݵķ����ǣ� ��
A.ֱ�ӹ۲�B.ʵ��C.����D.����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��k1x��b��ͼ����x�ύ�ڵ�A����3��0������y�ύ�ڵ�B����������������y��kx��ͼ��ΪC��3��4����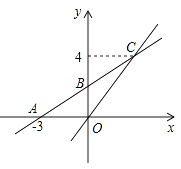
��1����������������һ�κ����Ĺ�ϵʽ��
��2������D�ڵڶ����ޣ���DAB����ABΪֱ�DZߵĵ���ֱ�������Σ��������D�����ꣻ
��3����x�����Ƿ����һ��Eʹ��BCE�ܳ���С�������ڣ������E������
��4����x������һ��Pʹ��POCΪ���������Σ���ֱ��д�����з��������ĵ�P�����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
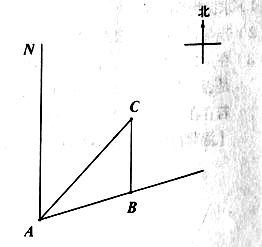
����Ŀ����ͼ��һ�Ҵ���ÿСʱ30������ٶ���ƫ��75�������У��ڵ�![]() �������ͷ
�������ͷ![]() �Ĵ��Ķ���������40���Ӻ�
�Ĵ��Ķ���������40���Ӻ�![]() ������ʱ��ͷ
������ʱ��ͷ![]() ǡ���ڴ������������ڴ����ı亽�������£�������ں��й���������ͷ
ǡ���ڴ������������ڴ����ı亽�������£�������ں��й���������ͷ![]() ���������.�������ȷ��0��1����ο�����
���������.�������ȷ��0��1����ο�����![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com