
����Ŀ����ͼ����ƽ��ֱ������ϵxOy�У�һ�κ���y��k1x��b��ͼ����x�ύ�ڵ�A����3��0������y�ύ�ڵ�B����������������y��kx��ͼ��ΪC��3��4����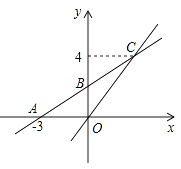
��1����������������һ�κ����Ĺ�ϵʽ��
��2������D�ڵڶ����ޣ���DAB����ABΪֱ�DZߵĵ���ֱ�������Σ��������D�����ꣻ
��3����x�����Ƿ����һ��Eʹ��BCE�ܳ���С�������ڣ������E������
��4����x������һ��Pʹ��POCΪ���������Σ���ֱ��д�����з��������ĵ�P�����꣮
���𰸡�
��1���⣺��һ�κ���y��k1x��b����A����3��0��; C��3��4��
�� ![]() ��ã�
��ã� 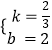
��һ�κ�����ϵʽΪy�� ![]() x��2
x��2
������������y��kx��ͼ�����ΪC��3��4��
��4=-3k2
��k2= ![]() ����������:y��
����������:y�� ![]() x
x
��2���⣺��ͼ��ʾ����D1M��X����M�㣬��D2N��Y����N���ڵ�����AD1B�У�
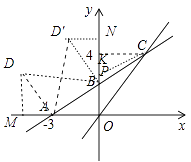
A D1=AB ; ��D1AB=90�� ��D1DA=��AOB=90��
���D1AM+��BAO=90�� �֡ߡ�ABO+��BAO=90��
���D1AM =��BAO
�ڡ�D1DA��� OAB��
��D1AM =��BAO����֤��
��D1MA=��AOB����֤��
A D1=AB ����֤��
���D1MA�ա�OAB��AAS��
��D1 M=OA=3;AM=BO=2 ��OM=5
��D1�ڵڶ����ޣ���D1(-5,3)
ͬ��֤����D2NB�ա�BOA��AAS�� ��D2(-2,5)
��3���⣺����;��C����X��ԳƵ�C1������BC1����X����E����ʱ��BCE�ܳ���С��
�� ![]() ��
�� ![]()
��BC1�Ľ���ʽΪ��y=-2x+2
��y=0����0=-2x+2, x=1
��E���������1��0��
��4���⣺P ��5��0��
P ��-5��0��
P (6, 0)
P ( ![]() ,0)
,0)
����������4���ٵ�OC������O�Ƕ��ǵĶ���ʱ��OP=OC�����P������Ϊ��5��0����-5��0����
�ڵ�OC������C�Ƕ��ǵĶ���ʱ��CP=CP�����P���O����x=3�Գƣ����P������Ϊ��6��0����
�۵�OC�ǵױ�ʱ�����P������Ϊ��a��0������a-3��2+42=a2�����a=![]() �����P������Ϊ��
�����P��������![]() ��0��.
��0��.
���Ͽ�֪����P�����꣨5��0����-5��0����6��0����![]() ��0��.
��0��.
�����㾫����������Ĺؼ���������һ�κ��������ʵ����֪ʶ������һ��أ�һ�κ���y=kx+b���������ʣ���1����k>0ʱ��y��x�����������2����k<0ʱ��y��x���������С���Լ���һ�κ�����ͼ������ʵ����⣬�˽�һ�κ�����ֱ�ߣ�ͼ�������ޣ���������������,����ԭ��һֱ�ߣ�����ϵ��k��b,����֮��ĪС����k��б�ʶ��н�,b��Y�������,kΪ��������б,x����y������kΪ��������չ,�仯�������෴��k�ľ���ֵԽ��,��������ԽԶ��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
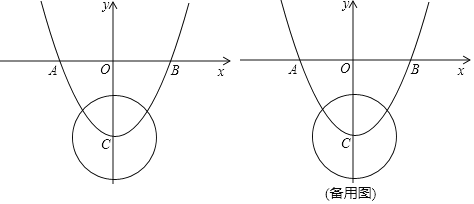
����Ŀ����ͼ����֪���κ���![]() ��ͼ����
��ͼ����![]() �ύ��
�ύ��![]() ������
������![]() �ύ�ڵ�
�ύ�ڵ�![]() ����
����![]() �İ뾶Ϊ
�İ뾶Ϊ![]() Ϊ��
Ϊ��![]() ��һ����.
��һ����.
��1����![]() ������ֱ�Ϊ
������ֱ�Ϊ![]() �� ����
�� ����![]() �� ����
�� ����
��2���Ƿ���ڵ�![]() ��ʹ��
��ʹ��![]() Ϊֱ�������Σ������ڣ������
Ϊֱ�������Σ������ڣ������![]() �����ꣻ�������ڣ���˵�����ɣ�
�����ꣻ�������ڣ���˵�����ɣ�
(3)����![]() ����
����![]() Ϊ
Ϊ![]() ���е㣬����
���е㣬����![]() ����
����![]() �����ֵ= .
�����ֵ= .
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУΪ�˽�ȫУѧ�������š����������������֡�Ϸ��������ӽ�Ŀ��ϲ����������ѡȡ��У����ѧ�����е��飬Ҫ��ÿ��ѧ������ֻѡһ����ϲ���ĵ��ӽ�Ŀ.�����Ǹ��ݵ��������Ƶ�ͳ��ͼ����һ����.
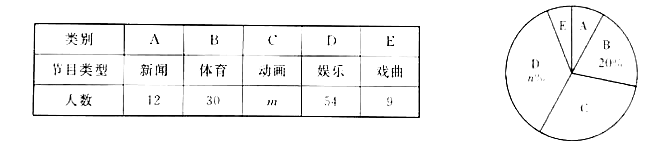
����������Ϣ������������⣺
��1���������ѧ���У���ϲ��������Ŀ���� �ˣ���Щѧ����ռ�������������İٷֱ�Ϊ %��
��2��������ѧ��������Ϊ �ˣ�ͳ�Ʊ���![]() ��ֵΪ ��ͳ��ͼ��
��ֵΪ ��ͳ��ͼ��![]() ��ֵΪ ��
��ֵΪ ��
��3����ͳ��ͼ�У�![]() ������Ӧ����Բ�ĽǵĶ���Ϊ ��
������Ӧ����Բ�ĽǵĶ���Ϊ ��
��4����У����2000��ѧ�������ݵ����������Ƹ�У��ϲ����ο��Ŀ��ѧ����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У��ı���![]() �Ķ���
�Ķ���![]() ������ԭ�㣬��
������ԭ�㣬��![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() ������Ϊ
������Ϊ![]() ����
����![]() �ֱ�Ϊ�ı���
�ֱ�Ϊ�ı���![]() ���ϵĶ��㣬����
���ϵĶ��㣬����![]() �ӵ�
�ӵ�![]() ��ʼ����ÿ��1����λ���ȵ��ٶ���
��ʼ����ÿ��1����λ���ȵ��ٶ���![]() ·�����е�
·�����е�![]() �����˶�������
�����˶�������![]() ��
��![]() �㿪ʼ����ÿ��������λ���ȵ��ٶ���
�㿪ʼ����ÿ��������λ���ȵ��ٶ���![]() ·�����յ�
·�����յ�![]() �����˶�����
�����˶�����![]() ͬʱ��
ͬʱ��![]() �������������һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶����趯���˶���ʱ��
�������������һ�㵽���յ����һ��Ҳ��ֹ֮ͣ�˶����趯���˶���ʱ��![]() ����
����![]() ����
����![]() �����Ϊ
�����Ϊ![]() .
.
��1����գ�![]() �ij��� ��
�ij��� ��![]() �ij��� ��
�ij��� ��
��2����![]() ʱ����
ʱ����![]() ��ֵ��
��ֵ��
��3����![]() ʱ�����
ʱ�����![]() ��������Ϊ
��������Ϊ![]() ����
����![]() ��
��![]() �ĺ�����ϵʽ��
�ĺ�����ϵʽ��
��4����![]() ����ֱ��д����ʱ
����ֱ��д����ʱ![]() ��ֵ.
��ֵ.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪y+1��x+3�����������ҵ�x=5ʱ��y=3
��1���� ![]() ��
�� ![]() ֮��ĺ�����ϵʽ����
֮��ĺ�����ϵʽ����
��2���� ![]() ʱ����
ʱ���� ![]() ��ֵ.
��ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() �ֱ���
�ֱ���![]() ���е㣬��
���е㣬��![]() Ϊб����
Ϊб����![]() ����
����![]() �������н��۲���ȷ������ ��
�������н��۲���ȷ������ ��
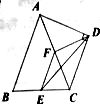
A�� ![]() B��
B��![]() ƽ��
ƽ��![]() C.
C. ![]() D��
D��![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������һ��������ľ�䣬������һ�������Σ���Ϊ3m�����Ϊ4.32m3�����ľ��ĵ����ܳ���
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com