
【题目】如图,已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点与
两点与![]() 轴交于点
轴交于点![]() ,⊙
,⊙![]() 的半径为
的半径为![]() 为⊙
为⊙![]() 上一动点.
上一动点.
(1)点![]() 的坐标分别为
的坐标分别为![]() ( ),
( ),![]() ( );
( );
(2)是否存在点![]() ,使得
,使得![]() 为直角三角形?若存在,求出点
为直角三角形?若存在,求出点![]() 的坐标;若不存在,请说明理由;
的坐标;若不存在,请说明理由;
(3)连接![]() ,若
,若![]() 为
为![]() 的中点,连接
的中点,连接![]() ,则
,则![]() 的最大值= .
的最大值= .
【答案】(1)3,0;0,-4;(2)(-1,-2)或((![]() ,
,![]() ),或(
),或(![]() ,-
,-![]() -4)或(--
-4)或(--![]() ,
,![]() );(3)
);(3)![]() .
.
【解析】
试题分析:(1)在抛物线解析式中令y=0可求得B点坐标,令x=0可求得C点坐标;
(2)①当PB与⊙相切时,△PBC为直角三角形,如图1,连接BC,根据勾股定理得到BC=5,BP2=2![]() ,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到
,过P2作P2E⊥x轴于E,P2F⊥y轴于F,根据相似三角形的性质得到![]() ,设OC=P2E=2x,CP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=
,设OC=P2E=2x,CP2=OE=x,得到BE=3-x,CF=2x-4,于是得到FP2=![]() ,EP2=
,EP2=![]() ,求得P2(
,求得P2(![]() ,-
,-![]() ),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
),过P1作P1G⊥x轴于G,P1H⊥y轴于H,同理求得P1(-1,-2),②当BC⊥PC时,△PBC为直角三角形,根据相似三角形的判定和性质即可得到结论;
(3)如图2,当PB与⊙C相切时,OE的值最大,过E作EM⊥y轴于M,过P作PF⊥y轴于F,根据平行线等分线段定理得到ME=![]() (OB+PF)=
(OB+PF)=![]() ,OM=MF=
,OM=MF=![]() OF=
OF=![]() ,根据勾股定理即可得到结论.
,根据勾股定理即可得到结论.
试题解析:(1)在y=![]() x2-4中,令y=0,则x=±3,令x=0,则y=-4,
x2-4中,令y=0,则x=±3,令x=0,则y=-4,
∴B(3,0),C(0,-4);
(2)存在点P,使得△PBC为直角三角形,
①当PB与⊙相切时,△PBC为直角三角形,如图(2)a,连接BC,
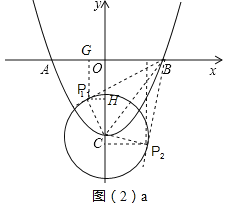
∵OB=3.OC=4,
∴BC=5,
∵CP2⊥BP2,CP2=![]() ,
,
∴BP2=2![]() ,
,
过P2作P2E⊥x轴于E,P2F⊥y轴于F,则△CP2F∽△BP2E,四边形OCP2B是矩形,
∴![]() ,
,
设OC=P2E=2x,CP2=OE=x,
∴BE=3-x,CF=2x-4,
∴![]() ,
,
∴x=![]() ,2x=
,2x=![]() ,
,
∴FP2=![]() ,EP2=
,EP2=![]() ,
,
∴P2(![]() ,
,![]() ),
),
过P1作P1G⊥x轴于G,P1H⊥y轴于H,
同理求得P1(-1,-2),
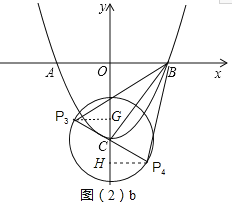
②当BC⊥PC时,△PBC为直角三角形,过P4作P4H⊥y轴于H,则△BOC∽△CHP4,
∴![]() ,
,
∴CH=![]() ,P4H=
,P4H=![]() ,
,
∴P4(![]() ,-
,-![]() -4);
-4);
同理P3(-![]() ,
,![]() );
);
综上所述:点P的坐标为:(-1,-2)或((![]() ,
,![]() ),或(
),或(![]() ,-
,-![]() -4)或(--
-4)或(--![]() ,
,![]() );
);
(3)如图(3),当PB与⊙C相切时,PB与y 轴的距离最大,OE的值最大,
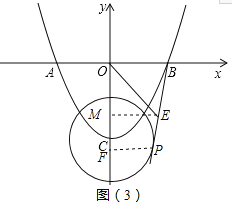
∵过E作EM⊥y轴于M,过P作PF⊥y轴于F,
∴OB∥EM∥PF,
∵E为PB的中点,
∴ME=![]() (OB+PF)=
(OB+PF)=![]() ,OM=MF=
,OM=MF=![]() OF=
OF=![]() ,
,
∴OE=![]() .
.


 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案 新卷王期末冲刺100分系列答案
新卷王期末冲刺100分系列答案 全能闯关100分系列答案
全能闯关100分系列答案科目:初中数学 来源: 题型:
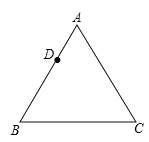
【题目】如图,已知等边△ABC,请用直尺(不带刻度)和圆规,按下列要求作图(不要求写作法,但要保留作图痕迹):
(1)作△ABC的外心O;
(2)设D是AB边上一点,在图中作出一个正六边形DEFGHI,使点F,点H分别在边BC和AC上.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平面直角坐标系中,每个小正方形边长都是1.
(1)按要求作图:
①△ABC关于x轴对称的图形△ ![]() ;
;
②将△ ![]() 向右平移6个单位得到△
向右平移6个单位得到△ ![]() .
.
(2)回答下列问题:
①△ ![]() 中顶点B2坐标为 .
中顶点B2坐标为 .
②若 ![]() 为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
为△ABC边上一点,则按照(1)中①、②作图,点P对应的点P2的坐标为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知y是x 的函数,自变量x的取值范围是x >0,下表是y与x 的几组对应值.
x | ··· | 1 | 2 | 3 | 5 | 7 | 9 | ··· |
y | ··· | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | ··· |
小腾根据学习一次函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系 ![]() 中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;
中,描出了以上表中各对对应值为坐标的点.根据描出的点,画出该函数的图象;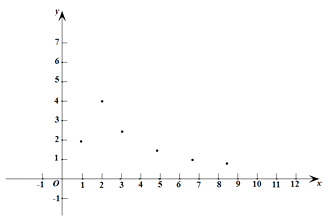
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为;
②该函数的一条性质: .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,△ABC的顶点分别为A(-4, 5),B(﹣3, 2),C(4,-1).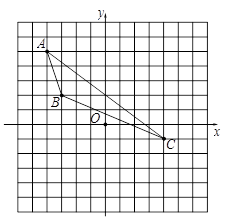
(1)作出△ABC关于x轴对称的图形△A1B1C1;
(2)写出A1、B1、C1的坐标;
(3)若AC=10,求△ABC的AC边上的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,一次函数y=k1x+b的图象与x轴交于点A(-3,0),与y轴交于点B,且与正比例函数y=kx的图象交点为C(3,4).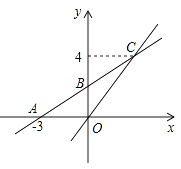
(1)求正比例函数与一次函数的关系式;
(2)若点D在第二象限,△DAB是以AB为直角边的等腰直角三角形,请求出点D的坐标;
(3)在x轴上是否存在一点E使△BCE周长最小,若存在,求出点E的坐标
(4)在x轴上求一点P使△POC为等腰三角形,请直接写出所有符合条件的点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com